题目内容
圆(x+
)2+(y+1)2=
与圆(x-sinθ)2+(y-1)2=
(θ为锐角)的位置关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
| A、相离 | B、外切 | C、内切 | D、相交 |
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:求出两个圆的圆心与半径,通过圆心距与半径和与差的关系判断选项即可.
解答:
解:圆(x+
)2+(y+1)2=
的圆心(-
,-1),半径为:
;
圆(x-sinθ)2+(y-1)2=
的圆心(sinθ,1),半径为:
,
圆心距为:
=
>2,
半径和:
<2,
两个圆相离.
故选:A.
| 1 |
| 2 |
| 8 |
| 16 |
| 1 |
| 2 |
| ||
| 2 |
圆(x-sinθ)2+(y-1)2=
| 1 |
| 16 |
| 1 |
| 4 |
圆心距为:
(sinθ+
|
(sinθ+
|
半径和:
1+2
| ||
| 4 |
两个圆相离.
故选:A.
点评:本题考查两个圆的位置关系,两点间距离公式的应用,考查计算能力.

练习册系列答案
相关题目
用min{a,b)表示a,b两数中的最小值.若函数f(x)=min{|x|,|x+t|}-
恰有三个零点,则t的值为( )
| 1 |
| 2 |
| A、-2 | B、2 |
| C、2或-2 | D、1或-l |
下列各式的导数计算正确的是( )
A、(lgx)′=
| ||
B、(ln5)′=
| ||
| C、(x2sinx)′=2xcosx | ||
| D、(3x)′=3xln3 |
某几何体的三视图如图所示,则该几何体的表面积为( )
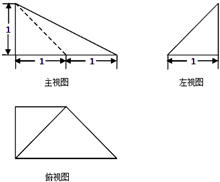

A、3+
| ||||||||
B、3+
| ||||||||
C、3+
| ||||||||
D、
|
化简
的结果是( )
| 1-sin260° |
| A、cos60° |
| B、-cos60° |
| C、±cos60° |
| D、±|cos60°| |
将参加冬季越野跑的600名选手编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,把编号分50组后,在第一组的001到012这12个编号中随机抽得的号码为004.这600名选手分别穿着三种颜色的衣服,从001到311穿红色衣服,从312到496穿白色衣服,从497到600穿黄色衣服.若从样本中任意抽取一个,则抽到穿白色衣服的选手的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
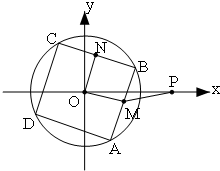 如图,已知点P(2,0),正方形ABCD内接于⊙O:x2+y2=2,M、N分别为边AB、BC的中点,当正方形ABCD绕圆心O旋转时,
如图,已知点P(2,0),正方形ABCD内接于⊙O:x2+y2=2,M、N分别为边AB、BC的中点,当正方形ABCD绕圆心O旋转时,| PM |
| ON |
| A、[-1,1] | ||||||||
B、[-
| ||||||||
| C、[-2,2] | ||||||||
D、[-
|
函数f(x)=log
(a-2x)-(2+x)有零点,则a的取值范围为( )
| 1 |
| 2 |
| A、(1,+∞) |
| B、[1,+∞) |
| C、(-∞,1] |
| D、(-∞,1) |