题目内容
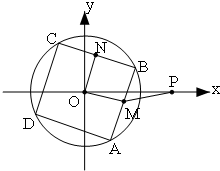 如图,已知点P(2,0),正方形ABCD内接于⊙O:x2+y2=2,M、N分别为边AB、BC的中点,当正方形ABCD绕圆心O旋转时,
如图,已知点P(2,0),正方形ABCD内接于⊙O:x2+y2=2,M、N分别为边AB、BC的中点,当正方形ABCD绕圆心O旋转时,| PM |
| ON |
| A、[-1,1] | ||||||||
B、[-
| ||||||||
| C、[-2,2] | ||||||||
D、[-
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:首先,根据
⊥
,设M(cosα,sinα),N(-sinα,cosα),然后,写出向量
=(cosα-2,sinα)和
=(-sinα,cosα),从而得到
•
=2sinα,进而确定其范围.
| OM |
| ON |
| PM |
| ON |
| PM |
| ON |
解答:
解:设M(cosα,sinα),
∵
⊥
,
∴
•
=0,
∴N(-sinα,cosα),
∴
=(-sinα,cosα),
=(cosα,sinα),
∴
=(cosα-2,sinα),
∴
•
=-sinα(cosα-2)+sinαcosα
=2sinα,
∵sinα∈[-1,1],
∴2sinα∈[-2,2],
∴
•
的取值范围是[-2,2].
故选:C.
∵
| OM |
| ON |
∴
| OM |
| ON |
∴N(-sinα,cosα),
∴
| ON |
| OM |
∴
| PM |
∴
| PM |
| ON |
=2sinα,
∵sinα∈[-1,1],
∴2sinα∈[-2,2],
∴
| PM |
| ON |
故选:C.
点评:本题重点考查了平面向量的实际运用,重点掌握平面向量的坐标运算等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
圆(x+
)2+(y+1)2=
与圆(x-sinθ)2+(y-1)2=
(θ为锐角)的位置关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
| A、相离 | B、外切 | C、内切 | D、相交 |
已知f(x)=x3-3x,则函数h(x)=f[f(x)]的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
某制药厂月生产A、B、C三种药品共4000件,为了保证产品质量,省质监局进行抽样检验,根据分层抽样的结果,省质监局的统计员制作了如下的统计表格:
由于不小心,表格中A、C产品扔关数据已被污染的看不清楚,统计员记得A产品的样本容量比C产品的样本容量多20,根据以上信息,可得C产品的样本容量是( )
| 产品类别 | A | B | C |
| 产品数量(件) | 1600 | ||
| 样本容量(件) | 160 |
| A、1300 | B、1100 |
| C、130 | D、110 |
在△ABC中,A:B:C=1:2:3,则sinA:sinB:sinC=( )
| A、1:2:3 | ||||
B、1:
| ||||
C、1:
| ||||
D、1:
|
设x,y满足约束条件
向量
=(y-2x,m),
=(1,1),且
∥
,则m的最小值为( )
|
| a |
| b |
| a |
| b |
| A、6 | ||
| B、-6 | ||
C、
| ||
D、-
|
执行如图所示的程序框图,则输出S=( )


| A、9 | B、10 | C、16 | D、25 |