Question

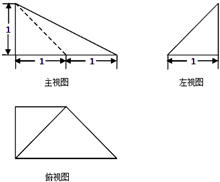
某几何体的三视图如图所示，则该几何体的表面积为（　　）

• A、3+

  2

  2

• B、3+

  6

  2

• C、3+

  2

  2

  +

  6

  2

• D、

  2

  2

  +

  6

  2

Answer 1

考点：由三视图求面积、体积

专题：计算题,空间位置关系与距离

分析：几何体是四棱锥，根据三视图判断几何体的结构特征及数据所对应的几何量，结合直观图求各个面的面积，再相加．

解答： 解：由三视图知：几何体是四棱锥，且四棱锥的一条侧棱与底面垂直，如图：
其中SA⊥平面ABCD，SA=1，底面ABCD是直角梯形，直角梯形的直角腰AD=1，两底边CD=1，AB=2，
∴SC=

1+2

=

3

，BC=

2

，SB=

5

，SD=

2

，
∴三角形SBC为直角三角形，
∴几何体的表面积S=

1

2

×1×1+

1

2

×1×2+

1

2

×

2

×1+

1

2

×

2

×

3

+

1+2

2

×1=3+

2 + 6

2

．
故选：C．

点评：本题考查了由三视图求几何体的表面积，根据三视图判断几何体的结构特征是解题的关键．