题目内容
过抛物线y=ax2（a＞0）的焦点F作一条斜率不为0的直线交抛物线于A、B两点，若线段AF、BF的长分别为m、n，则
等于（ ）
| mn |
| m+n |
A、
| ||
B、
| ||
| C、2a | ||
D、
|
考点：抛物线的简单性质
专题：圆锥曲线中的最值与范围问题
分析：根据抛物线方程可求得焦点坐标和准线方程，设过F的直线方程，与抛物线方程联立，整理后，设A（x1，y1），B（x2，y2）根据韦达定理可求得x1x2的值，又根据抛物线定义可知|AF|=y1+1，|BF|=y2+1代入答案可得．
解答：
解：易知F坐标（0，
）准线方程为x=-
．÷
设过F点直线方程为y=kx+
代入抛物线方程，得 ax2-kx-
=0．
设A（x1，y1），B（x2，y2）
则有x1x2=
，x1+x2=
，
∴y1+y2=k（x1+x2）+
=
+
，
y1y2=(kx1+
)(kx2+
)=
，
根据抛物线性质可知，m=y1+
，n=y2+
∴m+n=y1+y2+
=
，
mn=y1y2+
(y1+y2)+
=
，
∴
=
=
故选B．
| 1 |
| 4a |
| 1 |
| 4a |
设过F点直线方程为y=kx+
| 1 |
| 4a |
代入抛物线方程，得 ax2-kx-
| 1 |
| 4a |
设A（x1，y1），B（x2，y2）
则有x1x2=
| 1 |
| 4 |
| k |
| a |
∴y1+y2=k（x1+x2）+
| 1 |
| 2a |
| k2 |
| a |
| 1 |
| 2a |
y1y2=(kx1+
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 16a2 |
根据抛物线性质可知，m=y1+
| a |
| 4 |
| a |
| 4 |
∴m+n=y1+y2+
| a |
| 2 |
| k2+1 |
| a |
mn=y1y2+
| 1 |
| 4a |
| 1 |
| 16a2 |
=
| k2+1 |
| 4a2 |
∴
| mn |
| m+n |
| ||
|
| 1 |
| 4a |
故选B．
点评：本题主要考查抛物线的应用和抛物线定义．对于过抛物线焦点的直线与抛物线关系，常用抛物线的定义来解决．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
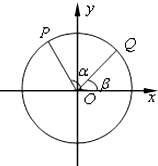如图，以Ox为始边作角α与β（0＜β＜α＜π），它们的终边分别与单位圆相交于点P、Q，已知点P的坐标为
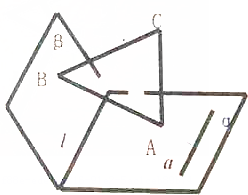如图，已知α∩β=l，CA⊥α于点A，CB⊥β于点B，a?α，a⊥AB，求证：a∥l．