Question

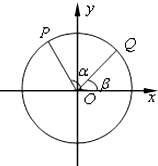如图，以Ox为始边作角α与β（0＜β＜α＜π），它们的终边分别与单位圆相交于点P、Q，已知点P的坐标为(-

4

5

，

3

5

)．
（1）求

sin2α-1-cos2α

(1-tanα)cosα

的值；
（2）若PQ=

2

，求sin（α+β）的值．

Answer 1

考点：任意角的三角函数的定义,两角和与差的正弦函数

专题：计算题,三角函数的求值

分析：（1）由三角函数的定义，再化简函数，即可得出结论；
（2）利用sin（α+β）=sinαcosβ+cosαsinβ，即可得出结论．

解答： 解：（1）由三角函数的定义得cosα=-

4

5

，sinα=

3

5

，…（2分）
则原式=

2sinαcosα-2cos2α

(1- sinα cosα )cosα

=

2cosα(sinα-cosα)

cosα-sinα

=-2cosα=-2×(-

4

5

)=

8

5

．…（6分）
（2）∵PQ=

2

，∴OP⊥OQ⇒α-β=

π

2

，
∴β=α-

π

2

，…（8分）
∴sinβ=sin(α-

π

2

)=-cosα=

4

5

，cosβ=cos(α-

π

2

)=sinα=

3

5

．…（10分）
∴sin（α+β）=sinαcosβ+cosαsinβ=

3

5

×

3

5

+(-

4

5

)×

4

5

=-

7

25

．…（14分）

点评：本题考查三角函数的定义，考查两角和与差的正弦函数，考查学生的计算能力，属于中档题．