题目内容
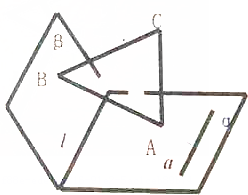 如图,已知α∩β=l,CA⊥α于点A,CB⊥β于点B,a?α,a⊥AB,求证:a∥l.
如图,已知α∩β=l,CA⊥α于点A,CB⊥β于点B,a?α,a⊥AB,求证:a∥l.考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:因为直线a,l在同一个平面内,a⊥AB,所以只要证明l⊥AB即可,进一步只要证明l⊥平面ABC即可.
解答:
证明:∵α∩β=l,CA⊥α于点A,CB⊥β于点B,
∴AC⊥l,CB⊥l,
∴l⊥平面ABC,
∴l⊥AB,
∵a⊥AB,a?α,l?α
∴a∥l.
∴AC⊥l,CB⊥l,
∴l⊥平面ABC,
∴l⊥AB,
∵a⊥AB,a?α,l?α
∴a∥l.
点评:本题考查了线面垂直判定定理和性质定理的运用以及线线平行的判断,关键是熟练线面垂直的有关定理,属于基础题

练习册系列答案
相关题目
过抛物线y=ax2(a>0)的焦点F作一条斜率不为0的直线交抛物线于A、B两点,若线段AF、BF的长分别为m、n,则
等于( )
| mn |
| m+n |
A、
| ||
B、
| ||
| C、2a | ||
D、
|
 如图有一个几何体的三视图(单位:cm),试画出它的直观图,并计算这个几何体的体积.
如图有一个几何体的三视图(单位:cm),试画出它的直观图,并计算这个几何体的体积.