题目内容
已知5x+12y=60,则xy的最大值为 .
考点:基本不等式
专题:不等式的解法及应用
分析:只考虑x,y>0时,利用基本不等式的性质即可得出.
解答:
解:只考虑x,y>0时,
∵5x+12y=60,∴60≥2
,
化为xy≤15,当且仅当5x=12y=30时取等号.
故答案为:15.
∵5x+12y=60,∴60≥2
| 5x•12y |
化为xy≤15,当且仅当5x=12y=30时取等号.
故答案为:15.
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
在等差数列{an}中,a3+a5=10,a7=2,则a1=( )
| A、5 | B、8 | C、10 | D、14 |
过点A(1,2)且与原点距离最大的直线方程为( )
| A、2x+y-4=0 |
| B、x+2y-5=0 |
| C、x+3y-7=0 |
| D、3x+y-5=0 |
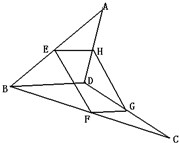 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.