题目内容
如图,在四棱锥P-ABCD中,∠ABC=∠BAD=90°AB=AD=2BC,△PAD为正三角形,且平面PAD⊥平面ABCD.

(Ⅰ)证明AD⊥PC
(Ⅱ)求二面角A-PD-C的余弦值.

(Ⅰ)证明AD⊥PC
(Ⅱ)求二面角A-PD-C的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AD的中点O,连接PO,OC,可证得四边形ABCO为矩形,结合等腰三角形三线合一及线面垂直的判定定理,可得AD⊥平面POC,进而AD⊥PC
(Ⅱ)(法一):分别以OC,OA,OP为x轴,y轴,z轴建立空间直角坐标系,分别求出平面APD,平面PDC的法向量,代入向量夹角公式,可求得二面角A-PD-C的余弦值.
(法二):过O点作OE⊥PD,垂足为E,连接CE,则CE⊥PD,于是∠CEO为所求二面角的一个平面角,解三角形可求得二面角A-PD-C的余弦值.
(Ⅱ)(法一):分别以OC,OA,OP为x轴,y轴,z轴建立空间直角坐标系,分别求出平面APD,平面PDC的法向量,代入向量夹角公式,可求得二面角A-PD-C的余弦值.
(法二):过O点作OE⊥PD,垂足为E,连接CE,则CE⊥PD,于是∠CEO为所求二面角的一个平面角,解三角形可求得二面角A-PD-C的余弦值.
解答:
证明:(Ⅰ)取AD的中点O,连接PO,OC,

∵△PAD为正三角形,
∴PO⊥AD…(2分),
又∵在四边形ABCD中,∠ABC=∠BAD=90°,AB=AD=2BC,
∴BC∥AO,且BC=AO
∴四边形ABCO为矩形,
∴CO⊥AD…(4分),
又∵PO∩CO=O,PO,CO?平面POC,
∴AD⊥平面POC,
又∵PC?平面POC,
∴AD⊥PC…(6分)
解:(Ⅱ)(法一):由(Ⅰ)知PO⊥AD,且平面PAD⊥平面ABCD
∴PO⊥平面ABCD,所以分别以OC,OA,OP为x轴,y轴,z轴建立如图所示的直角坐标系,并设BC=1,则AB=AD=2,OP=
,
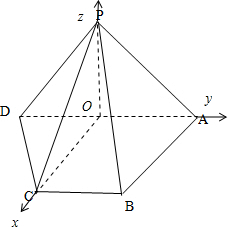
∴O(0,0,0),C(2,0,0),A(0,1,0),D(0,-1,0),P(0,0,
)
∴
=(0,0,
),
=(0,-1,0),
=(-2,0,
),
=(-2,-1,0)…(8分)
设平面APD,平面PDC的法向量分别为
=(x1,y1,z1),
=(x2,y2,z2)
则
且
∴
且
∴分别取平面APD,平面PDC的一个法向量
=(1,0,0),
=(
,-2
,2)…(10分)
∴cos<
,
>=
=
=
∴二面角A-PD-C的余弦值为
…(12分)
(法一):由(Ⅰ)知CO⊥AD,且平面PAD⊥平面ABCD
∴CO⊥平面PAD,
过O点作OE⊥PD,垂足为E,连接CE,则CE⊥PD,
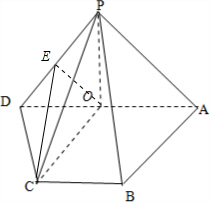
于是∠CEO为所求二面角的一个平面角,
设BC=1,则AB=AD=2,OD=1,OC=2,
则OE=
,CE=
=
,
∴cos∠OEC=
=
=
∴二面角A-PD-C的余弦值为
…(12分)

∵△PAD为正三角形,
∴PO⊥AD…(2分),
又∵在四边形ABCD中,∠ABC=∠BAD=90°,AB=AD=2BC,
∴BC∥AO,且BC=AO
∴四边形ABCO为矩形,
∴CO⊥AD…(4分),
又∵PO∩CO=O,PO,CO?平面POC,
∴AD⊥平面POC,
又∵PC?平面POC,
∴AD⊥PC…(6分)
解:(Ⅱ)(法一):由(Ⅰ)知PO⊥AD,且平面PAD⊥平面ABCD
∴PO⊥平面ABCD,所以分别以OC,OA,OP为x轴,y轴,z轴建立如图所示的直角坐标系,并设BC=1,则AB=AD=2,OP=
| 3 |

∴O(0,0,0),C(2,0,0),A(0,1,0),D(0,-1,0),P(0,0,
| 3 |
∴
| OP |
| 3 |
| OD |
| CP |
| 3 |
| CD |
设平面APD,平面PDC的法向量分别为
| n1 |
| n2 |
则
|
|
∴
|
|
∴分别取平面APD,平面PDC的一个法向量
| n1 |
| n2 |
| 3 |
| 3 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||
|
| ||
| 19 |
∴二面角A-PD-C的余弦值为
| ||
| 19 |
(法一):由(Ⅰ)知CO⊥AD,且平面PAD⊥平面ABCD
∴CO⊥平面PAD,
过O点作OE⊥PD,垂足为E,连接CE,则CE⊥PD,

于是∠CEO为所求二面角的一个平面角,
设BC=1,则AB=AD=2,OD=1,OC=2,
则OE=
| ||
| 2 |
| OC2+OE2 |
| ||
| 2 |
∴cos∠OEC=
| OE |
| CE |
| ||||
|
| ||
| 19 |
∴二面角A-PD-C的余弦值为
| ||
| 19 |
点评:本题考查的知识点是用空间向量求平面间的夹角,直线与平面垂直的判定与性质,是立体几何知识的综合考查,难度中档.

练习册系列答案
相关题目

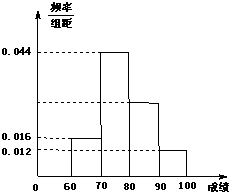 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图. 在棱长为2的正方体ABCD-A1B1C1D1中,O为正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=2PC.
在棱长为2的正方体ABCD-A1B1C1D1中,O为正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=2PC.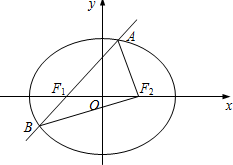 如图,椭圆E:
如图,椭圆E: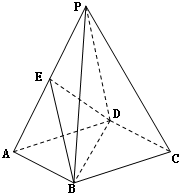 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证: