题目内容
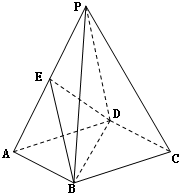如图，在四棱柱P-ABCD中，底面ABCD是矩形，E是棱PA的中点，PD⊥BC．求证：（I）PC∥平面BED；
（Ⅱ）BC⊥PC．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：（I）连接AC交BD于点O，连接OE．先证明出OE∥PC，进而根据线面平行的判定定理证明出 PC∥平面BDE．
（Ⅱ）先根据线面垂直的判定定理证明出BC⊥平面PDC，进而根据线面垂直的性质证明出BC⊥PC．
（Ⅱ）先根据线面垂直的判定定理证明出BC⊥平面PDC，进而根据线面垂直的性质证明出BC⊥PC．
解答：
证明：（Ⅰ）连接AC交BD于点O，连接OE．
在矩形ABCD中，AO=OC．
因为 AE=EP，
所以 OE∥PC．
因为 PC?平面BDE，OE?平面BDE，
所以 PC∥平面BDE．
（Ⅱ）在矩形ABCD中，BC⊥CD．
因为 PD⊥BC，CD∩PD=D，PD?平面PDC，DC?平面PDC，
所以 BC⊥平面PDC．
因为 PC?平面PDC，
所以 BC⊥PC．
在矩形ABCD中，AO=OC．
因为 AE=EP，
所以 OE∥PC．
因为 PC?平面BDE，OE?平面BDE，
所以 PC∥平面BDE．
（Ⅱ）在矩形ABCD中，BC⊥CD．
因为 PD⊥BC，CD∩PD=D，PD?平面PDC，DC?平面PDC，
所以 BC⊥平面PDC．
因为 PC?平面PDC，
所以 BC⊥PC．
点评：本题主要考查了直线与平面的平行的判定，直线与平面的垂直的判定．要求学生对定理能熟练掌握．
练习册系列答案
全能测控期末小状元系列答案
相关题目
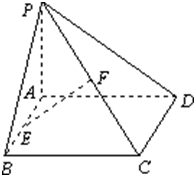已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、PC的中点，且PA=AD．
如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上．