题目内容
设Sn是数列{an}的前n项和,点P(an,Sn)在直线y=2x-2上
(1)求数列{an}的通项公式;
(2)记bn=2(1-
),数列{bn}的前n项和为Tn,若Tn≥a2-2恒成立,求a的最大值.
(1)求数列{an}的通项公式;
(2)记bn=2(1-
| 1 |
| an |
考点:数列的求和,数列的函数特性
专题:点列、递归数列与数学归纳法,不等式的解法及应用
分析:(1)把点的坐标代入直线方程得到数列递推式,进一步证得数列为等比数列,由等比数列的通项公式得答案;
(2)把(1)中求得的通项公式代入bn=2(1-
),由分组求和及等比数列的前n项和求得数列{bn}的前n项和为Tn,代入Tn≥a2-2后分离变量a,得到a2≤2[n+(
)n],由函数单调性求出2[n+(
)n]有最小值3,则a的最大值可求.
(2)把(1)中求得的通项公式代入bn=2(1-
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)依题意得Sn=2an-2,则n≥2时,
Sn-1=2an-1-2.
∴n≥2时,
Sn-Sn-1=2an-2an-1,
即an=2an-1.
又n=1时,a1=2,
∴数列{an}是以a1=2为首项,以2为公比的等比数列,
∴an=2•2n-1=2n;
(2)∵bn=2(1-
)=2(1-
)=2-
,
∴Tn=2n-(1+
+
+…+
)=2n-
=2n-2(1-
)=2n-2+2×(
)n.
由Tn≥a2-2恒成立,得2n-2+2×(
)n≥a2-2.
即a2≤2[n+(
)n].
令g(n)=n+(
)n,
∵g′(n)=1-(
)nln2>0,
∴g(n)=n+(
)n为增函数,
∴当n=1时,2[n+(
)n]有最小值3.
故a2≤3,解得-
≤a≤
.
∴a的最大值为
.
Sn-1=2an-1-2.
∴n≥2时,
Sn-Sn-1=2an-2an-1,
即an=2an-1.
又n=1时,a1=2,
∴数列{an}是以a1=2为首项,以2为公比的等比数列,
∴an=2•2n-1=2n;
(2)∵bn=2(1-
| 1 |
| an |
| 1 |
| 2n |
| 1 |
| 2n-1 |
∴Tn=2n-(1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
1-
| ||
1-
|
=2n-2(1-
| 1 |
| 2n |
| 1 |
| 2 |
由Tn≥a2-2恒成立,得2n-2+2×(
| 1 |
| 2 |
即a2≤2[n+(
| 1 |
| 2 |
令g(n)=n+(
| 1 |
| 2 |
∵g′(n)=1-(
| 1 |
| 2 |
∴g(n)=n+(
| 1 |
| 2 |
∴当n=1时,2[n+(
| 1 |
| 2 |
故a2≤3,解得-
| 3 |
| 3 |
∴a的最大值为
| 3 |
点评:本题考查等比关系的确定,考查了数列前n项和的求法,训练了分离变量法求解恒成立问题,属中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目

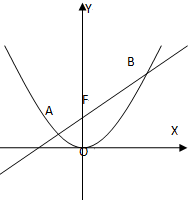 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点. 如图是正方体的平面展开图,则在这个正方体中,正确的是
如图是正方体的平面展开图,则在这个正方体中,正确的是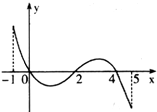 已知函数f(x)的定义域为[-1,5],部分对应值如图:
已知函数f(x)的定义域为[-1,5],部分对应值如图: