题目内容
已知函数f(x)=ln(x-1)-k(x-1)+1
(1)求函数f(x)的单调区间;
(2)若 f(x)≤0恒成立,式确定实数k的取值范围.
(1)求函数f(x)的单调区间;
(2)若 f(x)≤0恒成立,式确定实数k的取值范围.
考点:利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:本题(1)先求出函数的导函数,利用导函数值的正负,研究函数的单调性,注意要分类研究;(2)要使 f(x)≤0恒成立,就要求函数的最大值小于0,利用(1)的结论,得到求出函数最大值,得到相应的不等关系,解不等式,得到本题结论.
解答:
解:(1)∵函数f(x)=ln(x-1)-k(x-1)+1,
∴f′(x)=
-k,(x>1),
∴当k≤0时,f′(x)>0,∴函数f(x)在区间(1,+∞)上单调递增;
当k>0时,令
-k>0,则1<x<1+
,∴函数f(x)在区间(1,1+
)上单调递增;
令
-k<0,则x>1+
,∴函数f(x)在区间(1+
,+∞)上单调递减.
综上,当k≤0时,函数f(x)单调递增区间为(1,+∞);
当k>0时,函数f(x)单调递增区间为(1,1+
),单调递减区间为(1+
,+∞).
(2)由(1)知:当k>0时,函数f(x)的最大值为:f(1+
)=ln
=-lnk.
∵f(x)≤0恒成立,
∴-lnk<0,
∴k>1.
∴f′(x)=
| 1 |
| x-1 |
∴当k≤0时,f′(x)>0,∴函数f(x)在区间(1,+∞)上单调递增;
当k>0时,令
| 1 |
| x-1 |
| 1 |
| k |
| 1 |
| k |
令
| 1 |
| x-1 |
| 1 |
| k |
| 1 |
| k |
综上,当k≤0时,函数f(x)单调递增区间为(1,+∞);
当k>0时,函数f(x)单调递增区间为(1,1+
| 1 |
| k |
| 1 |
| k |
(2)由(1)知:当k>0时,函数f(x)的最大值为:f(1+
| 1 |
| k |
| 1 |
| k |
∵f(x)≤0恒成立,
∴-lnk<0,
∴k>1.
点评:本题考查了导数与函数的单调性、最值和恒成立问题,本题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合M={(x,y)|y=2x2-x-1},N={y|y=2x2-x-1},则M∩N( )
| A、∅ | B、M | C、N | D、不存在 |
设等差数列{an}的前n项和为Sn.若公差d<0,且|a7|=|a8|,则使Sn>0的最大正整数n是( )
| A、12 | B、13 | C、14 | D、15 |
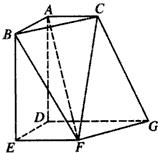 如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.
如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE= 执行如图所示的框图,若输入N=6,则输出的数S等于
执行如图所示的框图,若输入N=6,则输出的数S等于