题目内容
在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=3,则直线A1C与平面ABC1D1所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:计算题,空间位置关系与距离,空间角
分析:求出A1C,设直线A1C与平面ABC1D1所的交点为O,则O为中点,在直角△A1AD1中,过A1作A1H⊥AD1,垂足为H,连接OH,证得∠A1OH即为直线A1C与平面ABC1D1所成角,再解直角三角形A1OH,即可得到正弦值.
解答:
解:在长方体ABCD-A1B1C1D1中,A1C=
=
=
,
设直线A1C与平面ABC1D1所的交点为O,则O为A1C的中点,
即有A1O=
,在直角△A1AD1中,过A1作A1H⊥AD1,垂足为H,连接OH,
由AB⊥平面AD1,易得A1H⊥平面ABC1D1.
则∠A1OH即为直线A1C与平面ABC1D1所成角,
由于A1H=
=
,
即有sin∠A1OH=
=
×
=
.
故选A.
| AB2+AD2+AA12 |
| 1+4+9 |
| 14 |
设直线A1C与平面ABC1D1所的交点为O,则O为A1C的中点,
即有A1O=
| ||
| 2 |
由AB⊥平面AD1,易得A1H⊥平面ABC1D1.
则∠A1OH即为直线A1C与平面ABC1D1所成角,
由于A1H=
| A1A•A1D1 |
| AD1 |
| 3 | ||
|
即有sin∠A1OH=
| A1H |
| A1O |
| 3 | ||
|
| 2 | ||
|
3
| ||
| 35 |
故选A.
点评:本题考查直线与平面所成的角的求法,考查线面垂直的性质和判定,运算能力,属于中档题.

练习册系列答案
相关题目
已知向量
=(-1,-2,1),
=(2,x,3),若
⊥(
+
),则实数x的值为( )
| a |
| b |
| a |
| a |
| b |
A、-
| ||
| B、3 | ||
C、
| ||
D、
|
设等差数列{an}的前n项和为Sn.若公差d<0,且|a7|=|a8|,则使Sn>0的最大正整数n是( )
| A、12 | B、13 | C、14 | D、15 |
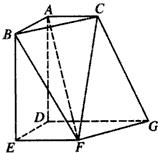 如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.
如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值. 执行如图所示的框图,若输入N=6,则输出的数S等于
执行如图所示的框图,若输入N=6,则输出的数S等于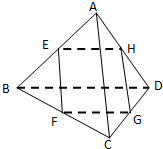 已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,
已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,