Question

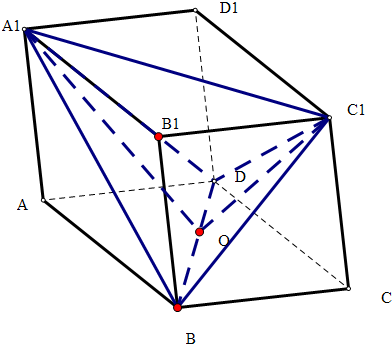
在正方体ABCD-A₁B₁C₁D₁中，平面A₁BD与平面C₁BD所成二面角的余弦值为（　　）

• A、

  1

  2

• B、

  1

  3

• C、

  3

  2

• D、

  3

  3

Answer 1

考点：二面角的平面角及求法

专题：空间位置关系与距离,空间角

分析：根据正方体分段性质得出∠A₁OC₁为平面A₁BD与平面C₁BD所成二面角的夹角，在△A₁OC₁中运用余弦定理求解即可．

解答： 解：取BD中的O，连接，OB，OA₁，A₁C₁，
∵在正方体ABCD-A₁B₁C₁D₁中，设棱长为1，
∴A₁C₁=

2

，OB=OA₁=

6

2

，
根据正方体的几何性质得出BD⊥OA，BD⊥OC，BD⊥AA₁，BD⊥CC₁，
∴BD⊥面OAA₁，BD⊥平面OCC₁，OA₁?面OAA₁，OC₁?平面OCC₁，
∴BD⊥OA₁，BD⊥OC₁，
∴∠A₁OC₁为平面A₁BD与平面C₁BD所成二面角的夹角，
∴在△A₁OC₁中，cos∠A₁OC₁=

3 2 + 3 2 -2

2× 6 2 × 6 2

=

1

3

故选：B

点评：本题考查了空间几何体的性质，空间角的求解，转化到三角形中求解，属于中档题，关键是确定角，求角．