题目内容
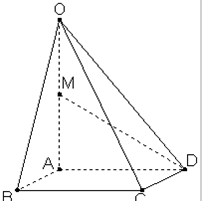 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.(1)求四棱锥O-ABCD的体积;
(2)求异面直线OC和MD所成角的正切值大小.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:综合题,空间角
分析:(1)四棱锥O-ABCD的底面是边长为2的正方形,高为2,由公式即可求得体积;
(2)根据异面直线所成角的定义作出OC和MD所成角再求出其大小即可得出所求的正切值.
(2)根据异面直线所成角的定义作出OC和MD所成角再求出其大小即可得出所求的正切值.
解答:
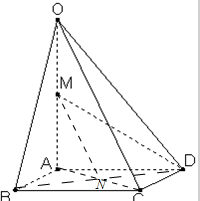 解:(1)由题意,四棱锥的底面积是2×2=4,高为2,故其体积为
解:(1)由题意,四棱锥的底面积是2×2=4,高为2,故其体积为
×4×2=
;
(2)连接AC,BD交于一点N,连接MN,ND,
由于N,M是中点,可得MN∥OC,所以∠NMD即为异面直线OC和MD所成角(或补角)
由已知OA⊥底面ABCD,底面ABCD是边长为2的正方形,可得Rt△MAD,Rt△MAN,Rt△MND
又由题设可得AM=1,DN=AN=
,在Rt△MAN中可得MN=
故tan∠NMD=
=
即异面直线OC和MD所成角的正切值大小为
.
 解:(1)由题意,四棱锥的底面积是2×2=4,高为2,故其体积为
解:(1)由题意,四棱锥的底面积是2×2=4,高为2,故其体积为| 1 |
| 3 |
| 8 |
| 3 |
(2)连接AC,BD交于一点N,连接MN,ND,
由于N,M是中点,可得MN∥OC,所以∠NMD即为异面直线OC和MD所成角(或补角)
由已知OA⊥底面ABCD,底面ABCD是边长为2的正方形,可得Rt△MAD,Rt△MAN,Rt△MND
又由题设可得AM=1,DN=AN=
| 2 |
| 3 |
故tan∠NMD=
| ||
|
| ||
| 3 |
即异面直线OC和MD所成角的正切值大小为
| ||
| 3 |
点评:本题考查异面直线所成的角及棱锥的体积的求解,线面垂直的定义等基础知识与技能属于立体几何中的基础题,要好好把握其解答规律.

练习册系列答案
相关题目
设集合M={(x,y)|y=2x2-x-1},N={y|y=2x2-x-1},则M∩N( )
| A、∅ | B、M | C、N | D、不存在 |
方程组
的解构成的集合是( )
|
| A、{(1,1)} |
| B、{1,1} |
| C、(1,1) |
| D、{1} |

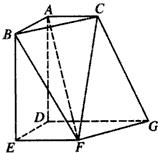 如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值.
如图,在空间中的Rt△ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.求二面角D-CG-F的余弦值. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,在侧面PBC内,有BE⊥PC于E,且BE=