题目内容
14.已知集合 P={x||x|>x},$Q=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,则 P∩Q=( )| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1] | D. | [0,1] |
分析 利用绝对值不等式的解法求出集合P,函数的定义域求出Q,然后求解交集.
解答 解:P={x||x|>x},={x|x<0},$Q=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,={x|x≤1},
P∩Q={x|x<0},
故选:A.
点评 本题考查集合的基本运算,不等式的解法,考查计算能力.

练习册系列答案
相关题目
15.下列说法不正确的一项是( )
| A. | 给定映射f:(x,y)→(2x+y,x-y),则在映射f元素(2,-1)与元素(3,3)可以对应; | |
| B. | 已知集合A={(x,y)|xy≥0},B={P|P是平面直角坐标系中的点},则f:A→B是映射; | |
| C. | 已知集合A={高三年级全体学生},集合B={0,1},对应关系f:A中的元素对应学生旱操出勤情况,如果早操出勤记为1,如果早操没有出勤记为0,则f:A→B是映射; | |
| D. | 已知函数f:M→N,则集合M是函数的定义域,集合N是函数的值域. |
3.已知x,y满足约束条件,$\left\{\begin{array}{l}{y≤1}\\{x+y-2≥0}\\{x-y-1≤0}\end{array}\right.$,则目标函数z=2x-y的最大值为( )
| A. | 1 | B. | 3 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.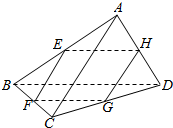 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.