题目内容
19.若直线l1:3x+y-3=0与l2:3x+my+1=0平行,则它们之间的距离为$\frac{2\sqrt{10}}{5}$.分析 由直线平行易得m值,可得方程,代入平行线间的距离公式可得.
解答 解:∵直线l1:3x+y-3=0与l2:3x+my+1=0平行,
∴m=1,
∴由距离公式可得所求距离d=$\frac{|1-(-3)|}{\sqrt{{3}^{2}+{1}^{2}}}$=$\frac{2\sqrt{10}}{5}$,
故答案为:$\frac{2\sqrt{10}}{5}$,
点评 本题考查直线的一般式方程与平行关系,属基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
20.已知集合A={y|y=x${\;}^{\frac{1}{3}}$,-1≤x≤1},B={y|y=2-$\frac{1}{x}$,0<x≤1},则集合A∪B=( )
| A. | (-∞,1] | B. | [-1,1] | C. | ∅ | D. | {1} |
14.已知集合 P={x||x|>x},$Q=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,则 P∩Q=( )
| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1] | D. | [0,1] |
4.已知函数f(x)=ax2+bx+3a+b为偶函数,其定义域为[a-3,2a],则a+b的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
11.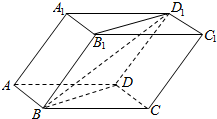 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
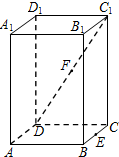 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: