Question

9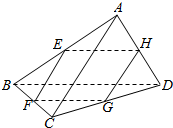．如图所示，在三棱锥A-BCD中，E，F，G，H分别是棱AB，BC，CD，DA的中点，则当AC，BD满足条件AC=BD时，四边形EFGH为菱形．

Answer 1

分析 由已知EH$\underset{∥}{=}$$\frac{1}{2}BD$$\underset{∥}{=}$FG，EF$\underset{∥}{=}$$\frac{1}{2}$AC$\underset{∥}{=}$HG，从而四边形EFGH为平行四边形，由四边形EFGH为菱形，得EF=EH，由此得到AC=BD．

解答 解：在三棱锥A-BCD中，
∵E，F，G，H分别是棱AB，BC，CD，DA的中点，
∴EH$\underset{∥}{=}$$\frac{1}{2}BD$，FG$\underset{∥}{=}$$\frac{1}{2}$BD，∴EH$\underset{∥}{=}$FG，
EF$\underset{∥}{=}$$\frac{1}{2}$AC，HG$\underset{∥}{=}$$\frac{1}{2}$AC，∴EF$\underset{∥}{=}$HG，
∴四边形EFGH为平行四边形，
∵四边形EFGH为菱形，∴EF=EH，∴AC=BD，
∴当AC，BD满足条件AC=BD时，四边形EFGH为菱形．
故答案为：AC=BD．

点评 本题考查四边形为菱形时需要具备条件的求法，是基础题，解题时要认真审题，注意三角形中位线定理和平行公理的合理运用．