题目内容
2. 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.(1)求证:平面PDC⊥平面PAD;
(2)若E是PD的中点,求异面直线AE与PC所成角的余弦值.
分析 (1)由PA⊥底面ABCD,底面ABCD是矩形,可得PA⊥CD及AD⊥CD,进而由线面垂直的判定定理得到DC⊥平面PAD,进而由面面垂直的判定定理得到平面PAD⊥平面PDC;
(2)以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,求出各顶点的坐标后,求出$\overrightarrow{AE}$,$\overrightarrow{PC}$,代入向量夹角公式即可求出异面直线AE与PC所成角的余弦值.
解答 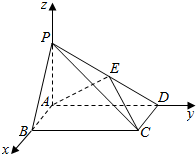 解:(1)∵PA⊥底面ABCD,CD?底面ABCD
解:(1)∵PA⊥底面ABCD,CD?底面ABCD
∴PA⊥CD.
∵底面ABCD是矩形,AD⊥CD.
又PA∩AD=A,AP?面PAD,AD?面PAD,
∴DC⊥平面PAD.
∵DC?平面PDC,
∴平面PAD⊥平面PDC,
(2)以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,则
A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,1),E(0,1,$\frac{1}{2}$).
∴$\overrightarrow{AE}$=(0,1,$\frac{1}{2}$),$\overrightarrow{PC}$=(1,2,-1),
∴$\overrightarrow{AE}$•$\overrightarrow{PC}$=0+2-$\frac{1}{2}$=$\frac{3}{2}$,|$\overrightarrow{AE}$|=$\frac{\sqrt{5}}{2}$,|$\overrightarrow{PC}$|=$\sqrt{6}$
设AE与PC所成角为θ,
∵cosθ=$\frac{\overrightarrow{AE}•\overrightarrow{PC}}{|\overrightarrow{AE}|•|\overrightarrow{PC}|}$=$\frac{\frac{3}{2}}{\frac{\sqrt{5}}{2}•\sqrt{6}}$=$\frac{\sqrt{30}}{10}$,
∴所求角的余弦值为$\frac{\sqrt{30}}{10}$.
点评 本题考查的知识点是利用空间向量求平面间的夹角,用空间向量求直线与平面的夹角,其中建立坐标系,将二面角及线面夹角问题转化为向量夹角问题是解答本题的关键.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1] | D. | [0,1] |
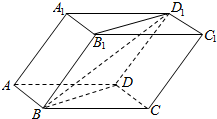 已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )
已知斜四棱柱ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,则异面直线BD1与AA1所成的角的余弦值为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{13}}{4}$ | C. | $\frac{\sqrt{39}}{13}$ | D. | $\frac{3}{4}$ |
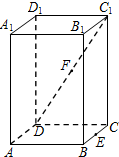 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: