题目内容
4.设函数f(x)=sin(ωx+ϕ),(ω>0,-π<ϕ<0)的两个相邻的对称中心分别为($\frac{π}{8}$,0),$(\frac{5π}{8},0)$(1)求f(x)的解析式;
(2)求函数f(x)图象的对称轴方程;
(3)用五点法作出函数f(x)在[0,π]上的简图.
分析 (1)由题意可求周期T,利用周期公式可求ω,由点($\frac{π}{8}$,0)在函数图象上,可得$0=sin(\frac{π}{4}+ϕ)$,结合范围-π<ϕ<0,可求ϕ,从而可求f(x)的解析式;
(2)由$2x-\frac{π}{4}=\frac{π}{2}+kπ$,可解得f(x)对称轴方程.
(3)分别取2x-$\frac{π}{4}$=0、$\frac{π}{2}$、π、$\frac{3π}{2}$、2π,求出对应的x值和y值列表,然后描点,再用平滑曲线连接得函数图象.
解答 解:(1)∵f(x)的两个相邻的对称中心分别为$(\frac{π}{8},0)$,$(\frac{5π}{8},0)$,
∴$T=\frac{4π}{8}×2=\frac{π}{2}×2=\frac{2π}{ω}=π$,
∴ω=2,
∴由$0=sin(\frac{π}{4}+ϕ)$,可得:$\frac{π}{4}+ϕ=kπ$,解得:$ϕ=kπ-\frac{π}{4}$,
∵-π<ϕ<0,
∴$ϕ=-\frac{π}{4}$,
∴$f(x)=sin(2x-\frac{π}{4})$.
(2)∵由$2x-\frac{π}{4}=\frac{π}{2}+kπ$,可得$2x=\frac{3π}{4}+kπ$,k∈Z,
∴f(x)对称轴方程为$x=\frac{3π}{8}+\frac{kπ}{2},k∈Z$
(3)第一步:列表
| x | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | $\frac{9π}{8}$ |
| 2x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y=sin(2x-$\frac{π}{4}$) | 0 | 1 | 0 | -1 | 0 |
第三步:连线画出图象如图所示:
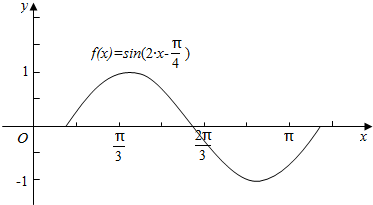
点评 本题考查了y=Asin(ωx+φ)型函数的有关概念,考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查利用五点作图法作函数的图象,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知集合 P={x||x|>x},$Q=\left\{{x\left|{y=\sqrt{1-x}}\right.}\right\}$,则 P∩Q=( )
| A. | (-∞,0) | B. | (0,1] | C. | (-∞,1] | D. | [0,1] |
15.已知:对任意x∈[0,1]都有$\sqrt{1-{x^2}}-cosωx≥0$成立,且ω>0则ω的取值范围为( )
| A. | $[\frac{π}{4},\frac{π}{2}]$ | B. | $(\frac{π}{4},\frac{π}{2}]$ | C. | $[\frac{π}{2},\frac{3π}{2}]$ | D. | $[\frac{π}{2},\frac{3π}{2})$ |