题目内容
1.求下列函数的定义域y=$\frac{1}{x-2}$+$\sqrt{2-(\frac{1}{2})^{x}}$.
分析 要使该函数有意义,则需满足$\left\{\begin{array}{l}{x-2≠0}\\{2-(\frac{1}{2})^{x}≥0}\end{array}\right.$,这样解该不等式即可得出该函数的定义域.
解答 解:解$\left\{\begin{array}{l}{x-2≠0}\\{2-(\frac{1}{2})^{x}≥0}\end{array}\right.$得,x≥-1,且x≠2;
∴该函数的定义域为{x|x≥-1,且x≠2}.
点评 考查函数定义域的概念及求法,以及指数函数的单调性.

练习册系列答案
相关题目
11.已知函数$f(x)=\left\{{\begin{array}{l}{\frac{1}{2}x+1,x≤2}\\{lnx,x>2}\end{array}}\right.$,方程f(x)-ax=0恰有3个不同实根,则实数a的取值范围是( )
| A. | $(\frac{ln2}{2},\frac{1}{e})$ | B. | $(0,\frac{1}{2})$ | C. | $(0,\frac{1}{e})$ | D. | $(\frac{1}{e},\frac{1}{2})$ |
9.已知x,y满足约柬条件$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$,当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,则$\frac{3}{a}$+$\frac{2}{b}$的最小值为( )
| A. | $\frac{25}{6}$ | B. | 4$+\sqrt{3}$ | C. | 4$+2\sqrt{3}$ | D. | 4$\sqrt{3}$ |
16.下列各组函数中,表示同一函数的是( )
| A. | y=$\sqrt{{x}^{2}}$和y=$(\sqrt{x})^{2}$ | B. | y=lg(x2-1)和y=lg(x+1)+lg(x-1) | ||
| C. | y=logax2和y=2logx | D. | y=x和y=logaax |
11.设函数f(x)=$\frac{1}{2}$x2-3x+31nx+3,则下列区间中有零点的是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
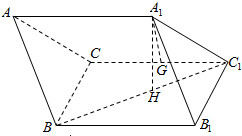 在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.
在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.