题目内容
12.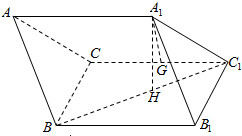 在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.
在三棱柱ABC-A1B1C1中,面BB1C1C是边长为2的正方形,点A1在平面BB1C1C上的射影H是BC1的中点,且A1H=$\sqrt{3}$,G是CC1的中点.(1)求证:BB1⊥A1G;
(2)求C到平面A1B1C1的距离.
分析 (1)连接GH,由已知得A1H⊥平面BB1C1C,可得A1H⊥BB1,由中位线和条件得BB1⊥HG,由线面垂直的判定定理可证结论成立;
(2)取B1C1的中点E,连接HE、A1E,由题意和线面垂直的判定定理、定义得B1C1⊥A1E,求出△A1B1C1的面积,由等体积法求出C到平面A1B1C1的距离.
解答  证明:(1)如图连接GH,
证明:(1)如图连接GH,
∵点A1在平面BB1C1C上的射影H,
∴A1H⊥平面BB1C1C,
∵BB1BC?平面BB1C1C,∴A1H⊥BB1,
∵H是BC1的中点,G是CC1的中点,
∴HG∥BC,
由∠B1BC=90°知,BB1⊥BC,∴BB1⊥HG
∵A1H∩HG=H,∴BB1⊥平面A1HG,
∴BB1⊥A1G;
解:(2)取B1C1的中点E,连接HE、A1E,
由∠BB1C1=90°得,HE⊥B1C1,
∵A1H⊥平面BB1C1C,∴A1H⊥B1C1,
∵A1H∩HE=H,∴B1C1⊥平面A1HE,∴B1C1⊥A1E,
∵H是BC1的中点,E是B1C1的中点,∴HE∥BB1,且HE=1,
在△A1HE中,A1E=$\sqrt{{A}_{1}{H}^{2}+H{E}^{2}}$=2,∴${S}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}$•B1C1AB•A1EBC=$\frac{1}{2}×2×2$=2,
设C到平面A1B1C1的距离为h,由${V}_{{A}_{1}-{B}_{1}{C}_{1}C}$=VA${V}_{{C-A}_{1}{B}_{1}{C}_{1}}$得,
$\frac{1}{3}$×A1E×${S}_{△{B}_{1}{C}_{1}C}$=$\frac{1}{3}$×h×${S}_{△{A}_{1}{B}_{1}{C}_{1}}$,
则$\frac{1}{3}×$$\sqrt{3}×$$\frac{1}{2}×$2×2=$\frac{1}{3}×$h×2,解得h=$\sqrt{3}$,
∴C到平面A1B1C1的距离是$\sqrt{3}$.
点评 本题考查空间位置关系及三棱锥的体积,考查线面垂直的判定定理、定义,及等体积法的应用,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{7}$ | D. | $\frac{2}{5}$ |
| A. | (0,$\sqrt{2}$) | B. | (0,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
| A. | [-1,0] | B. | [-1,2] | C. | [-1,3] | D. | [-1,4] |
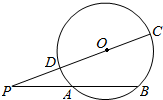 自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,
自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,