题目内容
给出定义在(0,+∞)上的三个函数:f(x)=lnx,g(x)=x2-af(x),h(x)=x-a
,已知g(x)在x=1处取极值.
(Ⅰ)求实数a的值,并确定函数h(x)的单调性;
(Ⅱ)求证:当1<x<e2时,恒有x<
成立;
(Ⅲ)若函数y=m-g(x)在[
,e]上有两个零点,求实数m的取值范围.
| x |
(Ⅰ)求实数a的值,并确定函数h(x)的单调性;
(Ⅱ)求证:当1<x<e2时,恒有x<
| 2+f(x) |
| 2-f(x) |
(Ⅲ)若函数y=m-g(x)在[
| 1 |
| e |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:求a的值通过g(x)在x=1处取得极值,则有g′(1)=0,所以能求出a的值.这样能求出h(x)的解析式,要确定h(x)的单调性,通过求导数判断导数符号的办法.对于第二问,恒有x<
成立,可以直接构造函数H(x)=x-
,然后判断该函数的单调性,看能否根据单调性证明F(x)<0.对于第三问求解的一般思路就是先计算函数在区间[
,e]取最值情况及函数在这一区间的单调性如何,从而得出对m的限制条件.
| 2+f(x) |
| 2-f(x) |
| 2+lnx |
| 2-lnx |
| 1 |
| e |
解答:
解:g(x)=x2-alnx,∴g′(x)=2x-
,∴g′(1)=2-a=0;
(Ⅰ)∴a=2,h(x)=x-2
,∴h′(x)=1-
;
∴x∈(0,1)时,h′(x)<0,∴h(x)在(0,1)上单调递减;
x∈(1,+∞)时,h′(x)>0,∴h(x)在(1,+∞)上单调递增.
(Ⅱ)要证x<
成立,∵1<x<e2,∴2-f(x)>0;
∴只要证(2-f(x))x<2+f(x),即证f(x)>
;
即证lnx-
>0;
设F(x)=lnx-
,则F′(x)=
>0,∴F(x)在(1,e2)上单调递增;
∴F(x)>F(1)=0,∴F(x)>0,∴lnx-
>0,∴当1<x<e2时,恒有x<
成立.
(Ⅲ)y=m-x2+2lnx,则y′=
;
∴函数y=m-x2+2lnx在[
,1)单调递增,在(1,e]单调递减;
∴该函数在x=1处取到极大值,也是最大值;
∴要使函数y=m-g(x)在[
,e]上有两个零点;
∵x=1时,y=m-1;
x=
时,y=m-
-2;
x=e时,y=m-e2+2,∴有:
;
∴解得:1<m≤
+2,即m的取值范围是(1,
+2].
| a |
| x |
(Ⅰ)∴a=2,h(x)=x-2
| x |
| 1 | ||
|
∴x∈(0,1)时,h′(x)<0,∴h(x)在(0,1)上单调递减;
x∈(1,+∞)时,h′(x)>0,∴h(x)在(1,+∞)上单调递增.
(Ⅱ)要证x<
| 2+f(x) |
| 2-f(x) |
∴只要证(2-f(x))x<2+f(x),即证f(x)>
| 2x-2 |
| x+1 |
即证lnx-
| 2x-2 |
| x+1 |
设F(x)=lnx-
| 2x-2 |
| x+1 |
| (x+3)(x-1) |
| x(x+1)2 |
∴F(x)>F(1)=0,∴F(x)>0,∴lnx-
| 2x-2 |
| x+1 |
| 2+f(x) |
| 2-f(x) |
(Ⅲ)y=m-x2+2lnx,则y′=
| 2(1-x2) |
| x2 |
∴函数y=m-x2+2lnx在[
| 1 |
| e |
∴该函数在x=1处取到极大值,也是最大值;
∴要使函数y=m-g(x)在[
| 1 |
| e |
∵x=1时,y=m-1;
x=
| 1 |
| e |
| 1 |
| e2 |
x=e时,y=m-e2+2,∴有:
|
∴解得:1<m≤
| 1 |
| e2 |
| 1 |
| e2 |
点评:考查的知识点为:利用导数判断函数的单调性,极值的概念,函数的最值.对于第二问,需要学会构造函数,判断函数的单调性,然后根据函数的单调性证明不等式.注意第三问所用的方法就是,先求函数在区间上的最值,根据是最大值还是最小值,通过限制闭区间两个端点值及最值的符号,从而求出m的取值范围.

练习册系列答案
相关题目
已知集合A={x|y=
},B={x∈Z|-2≤x≤4},则A∩B等于( )
| x |
| A、{0,1,2,3,4} |
| B、{x|0≤x≤4} |
| C、{-2,-1,0,1,2,3,4} |
| D、{2,3,4} |
f(x)=2x+3x的一个零点所在的一个区间是 ( )
| A、(1,2) |
| B、(0,1) |
| C、(-1,0) |
| D、(-2,-1) |
a>b>0,下列不等式一定成立的是( )
A、a+
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
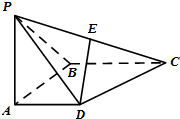 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点. 如图,在平面直角坐标系xOy中,点A(x1,y1)在单位圆O上,∠xOA=α,且α∈(
如图,在平面直角坐标系xOy中,点A(x1,y1)在单位圆O上,∠xOA=α,且α∈(