题目内容
某公司在一次年会上举行了有奖问答活动,会议组织者准备了10道题目,其中6道选择题,4道填空题,公司一职员从中任取3道题解答.
(1)求该职员至少取到1道填空题的概率;
(2)已知所取的3道题中有2道选择题,道填空题.设该职员答对选择题的概率都是
,答对每道填空题的概率都是
,且各题答对与否相互独立.用X表示该职员答对题的个数,求X的分布列和数学期望.
(1)求该职员至少取到1道填空题的概率;
(2)已知所取的3道题中有2道选择题,道填空题.设该职员答对选择题的概率都是
| 4 |
| 5 |
| 3 |
| 5 |
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)利用对立事件概率公式能求出该职员至少取到1道填空题的概率.
(2)由题意可知X的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
(2)由题意可知X的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答:
解:(1)设事件A=“该职员至少取到1道填空题”,
则有
=“该职员所取的3道题都是填空题”,
因为P(
)=
=
,
所以P(A)=1-P(
)=
.
∴该职员至少取到1道填空题的概率是
.…(4分)
(2)由题意可知X的所有可能取值为0,1,2,3.…(5分)
P(X=0)=
(
)0(
)2
=
…(6分)
P(X=1)=
(
)1(
)1
+
(
)0(
)2
=
,
P(X=2)=
(
)2(
)0
+
(
)1(
)1
=
,
P(X=3)=
(
)2(
)0
=
…(9分)
…(10分)
所以E(X)=0×
+1×
+2×
+3×
=
.…(12分)
则有
. |
| A |
因为P(
. |
| A |
| ||
|
| 1 |
| 6 |
所以P(A)=1-P(
. |
| A |
| 5 |
| 6 |
∴该职员至少取到1道填空题的概率是
| 5 |
| 6 |
(2)由题意可知X的所有可能取值为0,1,2,3.…(5分)
P(X=0)=
| C | 0 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 125 |
P(X=1)=
| C | 1 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| C | 0 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 19 |
| 125 |
P(X=2)=
| C | 2 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| C | 1 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 56 |
| 125 |
P(X=3)=
| C | 2 2 |
| 4 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 48 |
| 125 |
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
所以E(X)=0×
| 2 |
| 125 |
| 19 |
| 125 |
| 56 |
| 125 |
| 48 |
| 125 |
| 11 |
| 5 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期限,是中档题,在历年高考中考都是必考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
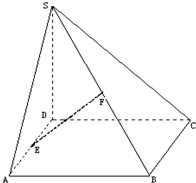 已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,
已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,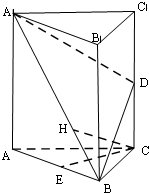 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.