题目内容
四边形ABCD为正方形,S为平面ABCD外的一点,S在底面ABCD上的射影为正方形的中心O,P为SD的中点,且SO=OD,求直线BC与截面PAC所成的角.
考点:直线与平面所成的角
专题:计算题,空间角
分析:以O为坐标原点,以OA为x轴,以OB为y轴,以OS为z轴,建立空间直角坐标系O-xyz,利用向量法求解.
解答:
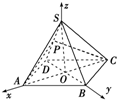 解:如图,以O为坐标原点,以OA为x轴,以OB为y轴,以OS为z轴,
解:如图,以O为坐标原点,以OA为x轴,以OB为y轴,以OS为z轴,
建立空间直角坐标系O-xyz.设OD=SO=OA=OB=OC=a,
则A(a,0,0),B(0,a,0),C(-a,0,0),P(0,-
,
),
则
=(2a,0,0),
=(-a,-
,
),
=(a,a,0),
设平面PAC的一个法向量为
,
则
,可取
=(0,1,1),
∴cos<
,
>=
=
,
∴<
,
>=60°,
∴直线BC与平面PAC的夹角为90°-60°=30°.
 解:如图,以O为坐标原点,以OA为x轴,以OB为y轴,以OS为z轴,
解:如图,以O为坐标原点,以OA为x轴,以OB为y轴,以OS为z轴,建立空间直角坐标系O-xyz.设OD=SO=OA=OB=OC=a,
则A(a,0,0),B(0,a,0),C(-a,0,0),P(0,-
| a |
| 2 |
| a |
| 2 |
则
| CA |
| AP |
| a |
| 2 |
| a |
| 2 |
| CB |
设平面PAC的一个法向量为
| n |
则
|
| n |
∴cos<
| CB |
| n |
| a | ||||
|
| 1 |
| 2 |
∴<
| CB |
| n |
∴直线BC与平面PAC的夹角为90°-60°=30°.
点评:此题重点考查了直线与平面所成的角的概念及利用空间向量的方法求解空间之中的直线与平面的夹角.

练习册系列答案
相关题目
下列各数中与1010(4)相等的数是( )
| A、1000100(2) |
| B、103(8) |
| C、2111(3) |
| D、76(9) |