题目内容
某人抛掷一枚硬币,出现正面、反面的概率均为
.构造数列{an},使得an=
,记Sn=a1+a2+a3+…+an(n∈N*).
(1)求S4=2的概率.
(2)若前两次均出现正面,求2≤S6≤6的概率.
| 1 |
| 2 |
|
(1)求S4=2的概率.
(2)若前两次均出现正面,求2≤S6≤6的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)先分析出S4=2对应的情况是4次中有3次正面、1次反面;再结合n次独立重复试验恰好出现k次的概率公式即可求出结论.
(2)根据条件前2次均出现正面,且2≤S6≤6,分析出对应的情况;再分别结合n次独立重复试验恰好出现k次的概率公式求出其概率,最后相加即可.
(2)根据条件前2次均出现正面,且2≤S6≤6,分析出对应的情况;再分别结合n次独立重复试验恰好出现k次的概率公式求出其概率,最后相加即可.
解答:
解:(1)某人抛掷一枚硬币4次,共有24种可能.
设S4=2为事件A,则A表示抛硬币4次,恰好三次正面向上,一次反面向上,包含4种可能,
所以P(A)=
=
.
(2)抛6次,若前两次均出现正面,则可能结果有24种.
设2≤S6≤6为事件B,S6=2表示4次中2次正面向上,2次正面向下,有6种可能;
S6=4表示4次中恰好3次正面向上,1次反面向上,有4种可能;
S6=6表示都是正面向上,有1种可能,则B包含6+4+1=11(种)可能,
所以P(B)=
=
.
设S4=2为事件A,则A表示抛硬币4次,恰好三次正面向上,一次反面向上,包含4种可能,
所以P(A)=
| 4 |
| 24 |
| 1 |
| 4 |
(2)抛6次,若前两次均出现正面,则可能结果有24种.
设2≤S6≤6为事件B,S6=2表示4次中2次正面向上,2次正面向下,有6种可能;
S6=4表示4次中恰好3次正面向上,1次反面向上,有4种可能;
S6=6表示都是正面向上,有1种可能,则B包含6+4+1=11(种)可能,
所以P(B)=
| 11 |
| 24 |
| 11 |
| 16 |
点评:本题考查概率的性质和应用,解题时要合理地运用n次独立重复试验恰好出现k次的概率公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知p:|x|<2;q:x2-x-2<0,则q是p的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
椭圆
+
=1的焦点坐标是( )
| x2 |
| m-2 |
| y2 |
| m+5 |
| A、(±7,0) | ||
| B、(0,±7) | ||
C、(±
| ||
D、(0,±
|
 已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号依次增加10进行系统抽样.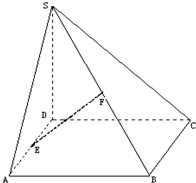 已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,
已知:如图,四棱锥S-ABCD底面为平行四边形,E、F分别为边AD、SB中点,