题目内容
已知函数f(x)=-
x3+2ax2+3x.
(1)当a=
时,求函数f(x)在[-2,2]上的最大值、最小值;
(2)令g(x)=ln(1-x)+3-f′(x),若g(x)在定义域上单调递减,求实数a的取值范围.
| 2 |
| 3 |
(1)当a=
| 1 |
| 4 |
(2)令g(x)=ln(1-x)+3-f′(x),若g(x)在定义域上单调递减,求实数a的取值范围.
考点:利用导数求闭区间上函数的最值,导数的运算,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)当a=
时,函数f(x)=-
x3+
x2+3x,f′(x)=-2x2+x+3=-(x+1)(2x-3),令f′(x)=0,解得x=-1,
.列出表格可得极值,再求出区间端点的函数值,经过比较即可得出最值.
(2)g(x)=ln(1-x)+3-f′(x)=ln(1-x)+,g(x)=ln(1-x)+2x2-4ax,由1-x>0可得其定义域为(-∞,1).
g′(x)=
+4x-4a=
.由于函数g(x)在定义域上单调递减,因此g′(x)≤0,x∈(-∞,1).即4x2-(4+4a)x+4a+1≥0恒成立,x∈(-∞,1)?a≥
,x∈(-∞,1).求出右边的最大值即可.
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
(2)g(x)=ln(1-x)+3-f′(x)=ln(1-x)+,g(x)=ln(1-x)+2x2-4ax,由1-x>0可得其定义域为(-∞,1).
g′(x)=
| 1 |
| x-1 |
| 4x2-(4+4a)x+4a+1 |
| x-1 |
| (2x-1)2 |
| 4(x-1) |
解答:
解:(1)当a=
时,函数f(x)=-
x3+
x2+3x,f′(x)=-2x2+x+3=-(x+1)(2x-3),
∵x∈[-2,2],令f′(x)=0,解得x=-1,
.
列表如下:
由表格可知:当x=-1时,函数f(x)取得极小值,f(-1)=-
,又f(2)=
,∴函数f(x)在区间[-2,2]的最小值为-
.当x=
时,函数f(x)取得极大值,f(
)=
,又f(-2)=
,∴函数f(x)在区间[-2,2]的最大值为
.
(2)g(x)=ln(1-x)+3-f′(x)=ln(1-x)+,g(x)=ln(1-x)+2x2-4ax,其定义域为(-∞,1).
g′(x)=
+4x-4a=
,
∵函数g(x)在定义域上单调递减,∴g′(x)≤0,x∈(-∞,1).
∴4x2-(4+4a)x+4a+1≥0恒成立,x∈(-∞,1).
?a≥
,x∈(-∞,1).
∵
≤0,∴a≥0.
因此实数a的取值范围是[0,+∞).
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
∵x∈[-2,2],令f′(x)=0,解得x=-1,
| 3 |
| 2 |
列表如下:
| x | [-2,-1) | -1 | (-1,
|
| (
| ||||||
| f′(x) | - | 0 | + | 0 | - | ||||||
| f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
| 11 |
| 6 |
| 8 |
| 3 |
| 11 |
| 6 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
| 4 |
| 3 |
| 27 |
| 8 |
(2)g(x)=ln(1-x)+3-f′(x)=ln(1-x)+,g(x)=ln(1-x)+2x2-4ax,其定义域为(-∞,1).
g′(x)=
| 1 |
| x-1 |
| 4x2-(4+4a)x+4a+1 |
| x-1 |
∵函数g(x)在定义域上单调递减,∴g′(x)≤0,x∈(-∞,1).
∴4x2-(4+4a)x+4a+1≥0恒成立,x∈(-∞,1).
?a≥
| (2x-1)2 |
| 4(x-1) |
∵
| (2x-1)2 |
| 4(x-1) |
因此实数a的取值范围是[0,+∞).
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了分离参数法求取值范围,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
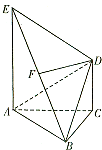 如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°.
如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°. 如图,已知点P在圆柱的底面圆O上,AB,A1B1分别为圆O,圆O1的直径.
如图,已知点P在圆柱的底面圆O上,AB,A1B1分别为圆O,圆O1的直径.