题目内容
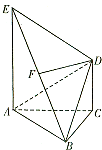 如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°.
如图,AE⊥平面ABC,CD∥AE,F是BE的中点,已知AC=BC=CD=1,AE=2,∠ACB=90°.(Ⅰ)证明:DF⊥平面ABE;
(Ⅱ)求二面角A-BD-C的正切值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:
分析:(Ⅰ)证明DF⊥平面ABE,只需证明CG⊥平面ABE,DF∥CG即可;
(Ⅱ)取BD的中点M,连接CM,连接AM,则BD⊥AM,所以∠ANC是二面角A-BD-C的平面角,即可求二面角A-BD-C的正切值.
(Ⅱ)取BD的中点M,连接CM,连接AM,则BD⊥AM,所以∠ANC是二面角A-BD-C的平面角,即可求二面角A-BD-C的正切值.
解答:
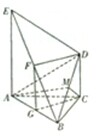 (Ⅰ)证明:取AB的中点G,连接CG、FG.
(Ⅰ)证明:取AB的中点G,连接CG、FG.
因为CD∥AE,GF∥AE,所以CD∥GF.
又因为CD=1,GF=
AE,所以CD=GF.
所以四边形CDFG是平行四边形,DF∥CG.(2分)
在等腰Rt△ACB中,G是AB的中点,所以CG⊥AB.
因为EA⊥平面ABC,CG?平面ABC,所以EA⊥CG.
而AB∩EA=A,所以CG⊥平面ABE.
又因为DF∥CG,所以DF⊥平面ABE;
(Ⅱ)解:因为AC⊥BC,AC⊥CD,BC∩CD=C,所以AC⊥平面BCD,
取BD的中点M,连接CM,则
因为BC=CD,所以CM⊥BD,
连接AM,则BD⊥AM,所以∠ANC是二面角A-BD-C的平面角,
因为BC=CD=1,BC⊥CD,所以CM=
BD=
,
因为AC=1,所以tan∠AMC=
=
,
所以二面角A-BD-C的正切值为
.
 (Ⅰ)证明:取AB的中点G,连接CG、FG.
(Ⅰ)证明:取AB的中点G,连接CG、FG.因为CD∥AE,GF∥AE,所以CD∥GF.
又因为CD=1,GF=
| 1 |
| 2 |
所以四边形CDFG是平行四边形,DF∥CG.(2分)
在等腰Rt△ACB中,G是AB的中点,所以CG⊥AB.
因为EA⊥平面ABC,CG?平面ABC,所以EA⊥CG.
而AB∩EA=A,所以CG⊥平面ABE.
又因为DF∥CG,所以DF⊥平面ABE;
(Ⅱ)解:因为AC⊥BC,AC⊥CD,BC∩CD=C,所以AC⊥平面BCD,
取BD的中点M,连接CM,则
因为BC=CD,所以CM⊥BD,
连接AM,则BD⊥AM,所以∠ANC是二面角A-BD-C的平面角,
因为BC=CD=1,BC⊥CD,所以CM=
| 1 |
| 2 |
| ||
| 2 |
因为AC=1,所以tan∠AMC=
| AC |
| CM |
| 2 |
所以二面角A-BD-C的正切值为
| 2 |
点评:本题考查线面垂直,考查二面角A-BD-C的平面角,正确运用线面垂直的判定定理,作出二面角的平面角是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设随机变量ξ服从正态分布N(2,σ 2),则方程x2+4x+2ξ=0无实数根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=
如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=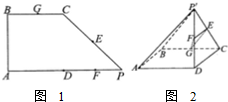 如图1所示,在直角梯形ABCP中,AP∥BC,AP⊥AB,AP=2AB=2BC,D是底边AP的中点,E.F、G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P位于点P′,且P′D⊥平面ABCD,得折叠后如图2的几何图形.
如图1所示,在直角梯形ABCP中,AP∥BC,AP⊥AB,AP=2AB=2BC,D是底边AP的中点,E.F、G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P位于点P′,且P′D⊥平面ABCD,得折叠后如图2的几何图形. 在长方体ABCD-A1B1C1D1中,已知AB=4,BC=3,CC1=5,求:
在长方体ABCD-A1B1C1D1中,已知AB=4,BC=3,CC1=5,求: