题目内容
如图，已知点P在圆柱的底面圆O上，AB，A1B1分别为圆O，圆O1的直径．（Ⅰ）求证：BP⊥A1P；
（Ⅱ）若该圆柱的体积V=12π，OA=2，∠AOP=
| 2 |
| 3 |
考点：与二面角有关的立体几何综合题,旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离,空间角
分析：（Ⅰ）由圆的性质得AP⊥BP，由线面垂直得AA1⊥BP，从而得到BP⊥平面PAA1，由此能证明BP⊥A1P．
（Ⅱ）以PB为x轴，PA为y轴．过P点的母线所在直线为Z轴建立空间直角坐标系，利用向量法能求出二面角P-A1B-A的余弦值．
（Ⅱ）以PB为x轴，PA为y轴．过P点的母线所在直线为Z轴建立空间直角坐标系，利用向量法能求出二面角P-A1B-A的余弦值．
解答：
（Ⅰ）证明：∵点P在圆柱的底面圆O上，AB，A1B1分别为圆O，圆O1的直径，
∴AP⊥BP，由AA1⊥平面PAB，
得AA1⊥BP，且AP∩AA1=A，
∴BP⊥平面PAA1，
故BP⊥A1P．…（5分）
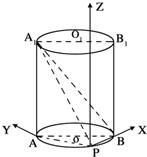（Ⅱ）解：如图建系（以PB为x轴，PA为y轴．过P点的母线所在直线为Z轴）
∵V柱=12π，OA=2，∴AA1=3，
由∠AOP=
π，知∠PAB=
，又∠APB=
，
从而BP=2，AP=2
，
∴P(0，0，0)，B(2，0，0)，A1(0，2
，3)，A(0，2
，0)，
设平面AA1B和法向量为
=(x1，y1，z1)，
由
知
=(
，1，0)
设平面PA1B的法向量为
=(x2，y2，z2)，
由
知
=(0，
，2)…（10分）
由题意知二面角P-A1B-A为锐二面角，
cosθ=|cos?
，
＞|=|
|=
因而所求二面角P-A1B-A的余弦值为
．…（12分）
∴AP⊥BP，由AA1⊥平面PAB，
得AA1⊥BP，且AP∩AA1=A，
∴BP⊥平面PAA1，
故BP⊥A1P．…（5分）
（Ⅱ）解：如图建系（以PB为x轴，PA为y轴．过P点的母线所在直线为Z轴）∵V柱=12π，OA=2，∴AA1=3，
由∠AOP=
| 2 |
| 3 |
| π |
| 6 |
| π |
| 2 |
从而BP=2，AP=2
| 3 |
∴P(0，0，0)，B(2，0，0)，A1(0，2
| 3 |
| 3 |
设平面AA1B和法向量为
| n1 |
由
|
| n1 |
| 3 |
设平面PA1B的法向量为
| n2 |
由
|
| n2 |
| 3 |
由题意知二面角P-A1B-A为锐二面角，
cosθ=|cos?
| n1 |
| n2 |
| ||
2
|
| ||
| 14 |
因而所求二面角P-A1B-A的余弦值为
| ||
| 14 |
点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
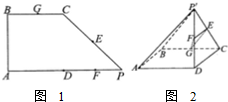如图1所示，在直角梯形ABCP中，AP∥BC，AP⊥AB，AP=2AB=2BC，D是底边AP的中点，E．F、G分别为PC、PD、CB的中点，将△PCD沿CD折起，使点P位于点P′，且P′D⊥平面ABCD，得折叠后如图2的几何图形．