题目内容
甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为
,乙获胜的概率为
,各局比赛结果相互独立.
(Ⅰ)求甲在4局以内(含4局)赢得比赛的概率;
(Ⅱ)记X为比赛决胜出胜负时的总局数,求X的分布列和均值(数学期望).
| 2 |
| 3 |
| 1 |
| 3 |
(Ⅰ)求甲在4局以内(含4局)赢得比赛的概率;
(Ⅱ)记X为比赛决胜出胜负时的总局数,求X的分布列和均值(数学期望).
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)根据概率的乘法公式,求出对应的概率,即可得到结论.
(2)利用离散型随机变量分别求出对应的概率,即可求X的分布列;以及均值.
(2)利用离散型随机变量分别求出对应的概率,即可求X的分布列;以及均值.
解答:
解:用A表示甲在4局以内(含4局)赢得比赛的是事件,Ak表示第k局甲获胜,Bk表示第k局乙获胜,
则P(Ak)=
,P(Bk)=
,k=1,2,3,4,5
(Ⅰ)P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)=(
)2+
×(
)2+
×
×(
)2=
.
(Ⅱ)X的可能取值为2,3,4,5.
P(X=2)=P(A1A2)+P(B1B2)=
,
P(X=3)=P(B1A2A3)+P(A1B2B3)=
,
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)=
,
P(X=5)=P(A1B2A3B4A5)+P(B1A2B3A4B5)+P(B1A2B3A4A5)+P(A1B2A3B4B5)=
=
,
或者P(X=5)=1-P(X=2)-P(X=3)-P(X=4)=
,
故分布列为:
E(X)=2×
+3×
+4×
+5×
=
.
则P(Ak)=
| 2 |
| 3 |
| 1 |
| 3 |
(Ⅰ)P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 56 |
| 81 |
(Ⅱ)X的可能取值为2,3,4,5.
P(X=2)=P(A1A2)+P(B1B2)=
| 5 |
| 9 |
P(X=3)=P(B1A2A3)+P(A1B2B3)=
| 2 |
| 9 |
P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)=
| 10 |
| 81 |
P(X=5)=P(A1B2A3B4A5)+P(B1A2B3A4B5)+P(B1A2B3A4A5)+P(A1B2A3B4B5)=
| 24 |
| 243 |
| 8 |
| 81 |
或者P(X=5)=1-P(X=2)-P(X=3)-P(X=4)=
| 8 |
| 81 |
故分布列为:
| X | 2 | 3 | 4 | 5 | ||||||||
| P |
|
|
|
|
| 5 |
| 9 |
| 2 |
| 9 |
| 10 |
| 81 |
| 8 |
| 81 |
| 224 |
| 81 |
点评:本题主要考查概率的计算,以及离散型分布列的计算,以及利用期望的计算,考查学生的计算能力.

练习册系列答案
相关题目
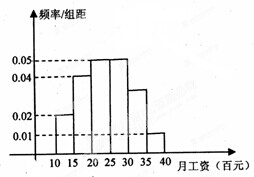 为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )
为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )| A、80 | B、150 |
| C、230 | D、400 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,
如图,三棱柱ABC-A1B1C1中,AA1⊥BC,A1B⊥BB1,(1)求证:A1C⊥CC1;
(2)若AB=2,AC=
| 3 |
| 7 |
某公司10位员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为
和s2,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
. |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|