题目内容
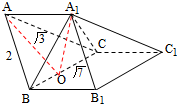
如图，三棱柱ABC-A1B1C1中，AA1⊥BC，A1B⊥BB1，（1）求证：A1C⊥CC1；
（2）若AB=2，AC=
| 3 |
| 7 |
考点：空间中直线与直线之间的位置关系,棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：（1）通过证明直线CC1与平面BA1C垂直，即可证明A1C⊥CC1；
（2）作AO⊥B 于O，连结A1O，说明∠AA1O=90°，设A1A=h，求出A1O的表达式，以及三棱柱ABC-A1B1C1体积V的表达式，利用二次函数的最值，求最大值．
（2）作AO⊥B 于O，连结A1O，说明∠AA1O=90°，设A1A=h，求出A1O的表达式，以及三棱柱ABC-A1B1C1体积V的表达式，利用二次函数的最值，求最大值．
解答：
解：（1）∵三棱柱ABC-A1B1C1中，
∴A1A∥CC1∥BB1，
∵AA1⊥BC，∴CC1⊥BC，
∵A1B⊥BB1，∴A1B⊥CC1，
∵BC∩BA1=B，
∴CC1⊥平面BA1C，A1C?平面BA1C
∴A1C⊥CC1；
（2）作AO⊥B 于O，连结A1O，由（1）可知∠AA1O=90°，∵AB=2，AC=
，BC=
，∴AB⊥AC，
∴AO=
，
设A1A=h，A1O=
=
，
∴三棱柱ABC-A1B1C1体积V=S△A1BC•h=
×
×
•h=
，
当h2=
，即h=
时，即AA1=
时棱柱的体积最大，
最大值为：
．
解：（1）∵三棱柱ABC-A1B1C1中，∴A1A∥CC1∥BB1，
∵AA1⊥BC，∴CC1⊥BC，
∵A1B⊥BB1，∴A1B⊥CC1，
∵BC∩BA1=B，
∴CC1⊥平面BA1C，A1C?平面BA1C
∴A1C⊥CC1；
（2）作AO⊥B 于O，连结A1O，由（1）可知∠AA1O=90°，∵AB=2，AC=
| 3 |
| 7 |
∴AO=
2
| ||
|
设A1A=h，A1O=
(
|
|
∴三棱柱ABC-A1B1C1体积V=S△A1BC•h=
| 1 |
| 2 |
| 7 |
|
| 1 |
| 2 |
| 12h2-7h4 |
当h2=
| 6 |
| 7 |
| ||
| 7 |
| ||
| 7 |
最大值为：
3
| ||
| 7 |
点评：本题考查空间直线与平面垂直的判定与应用，几何体的体积的最值的求法，考查转化思想以及空间想象能力．
练习册系列答案
相关题目
已知α、β、γ是三个不重合的平面，m、n是两条不重合的直线，下列命题为真命题的是（ ）
| A、m∥α，n∥α，则m∥n |
| B、α∥γ，n∥β，α∩β=m，则m∥n |
| C、α∥β，m?α，n?β，则m∥n |
| D、α∥γ，n?β，n?γ，α∩β=m，则m∥n |