题目内容
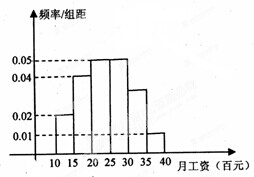为了解工薪阶层的收入情况，某地政府调查了1000人的月工资收入，并把调查结果画成如图所示的频率分布直方图，则由图知月工资在（30，35]（百元）的人数为（ ）| A、80 | B、150 |
| C、230 | D、400 |
考点：频率分布直方图
专题：概率与统计
分析：先有频率分布直方图求出在（30，35]（百元）收入段的频率，根据分层抽样的规则，用此频率乘以样本容量计算出应抽人数．
解答：
解：由图（30，35]（百元）收入段的频率是1-（0.02×5+0.04×5+0.05×5+0.05×5+0.01×5）=0.15．
故在（30，35]（百元）收入段应抽出人数为0.15×1000=150．
故选B．
故在（30，35]（百元）收入段应抽出人数为0.15×1000=150．
故选B．
点评：本题考查频率分布直方图与分层抽样的规则，解题的关键是从直方图中求得相应收入段的频率，再根据分层抽样的规则计算出样本中本收入段应抽的人数．
练习册系列答案
相关题目
已知α、β、γ是三个不重合的平面，m、n是两条不重合的直线，下列命题为真命题的是（ ）
| A、m∥α，n∥α，则m∥n |
| B、α∥γ，n∥β，α∩β=m，则m∥n |
| C、α∥β，m?α，n?β，则m∥n |
| D、α∥γ，n?β，n?γ，α∩β=m，则m∥n |
设F是双曲线
-
=1的焦点，过F作双曲线一条渐近线的垂线，与两条渐近线交于P，Q，若
=3
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| FQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某空间几何体的正视图是三角形，则该几何体不可能是（ ）
| A、圆柱 | B、圆锥 |
| C、四面体 | D、三棱柱 |