题目内容

4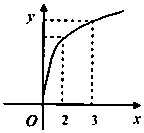．函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（　　）
A．0＜f′（2）＜f′（3）＜f（3）-f（2）B．0＜f′（3）＜f（3）-f（2）＜f′（2）C．0＜f′（3）＜f′（2）＜f（3）-f（2）D．0＜f（3）-f（2）＜f′（2）＜f′（3）

分析 由题意，作出f′（3）、f（3）-f（2）、f′（2）所表示的几何意义，从而求解．

解答 解：如下图：

f′（3）、f（3）-f（2）、f′（2）分别表示了直线n，m，l的斜率，
故0＜f′（3）＜f（3）-f（2）＜f′（2），
故选：B．

点评 本题考查了学生的作图能力及对导数的几何意义的理解，属于中档题．

练习册系列答案
相关题目
14．（Ⅰ）如果关于x的不等式|x+3|+|x-2|＜a的解集不是空集，求参数a的取值范围；
（Ⅱ）已知正实数a，b，且h=min{a，$\frac{b}{{a}^{2}+{b}^{2}}$}，求证：0＜h≤$\frac{\sqrt{2}}{2}$．
15．设函数f（x）是定义在（0，+∞）上的可导函数，其导函数为f′（x），f（x）＞0恒成立，且有2f（x）＞xf′（x）+x，则当x＞0时，下列不等关系一定正确的是（　　）
A．4xf（x2）≤x4f（2x）B．e2xf（$\frac{1}{x}$）≥$\frac{1}{{x}^{2}}$f（ex）
C．xf（$\sqrt{x}$）≤f（x）D．4xf（x+1）≤（x2+2x+1）f（2$\sqrt{x}$）
12．已知$tan（{x+\frac{π}{4}}）=\frac{1+tanx}{1-tanx}$，y=tanx的周期T=π，函数y=f（x）满足$f（{x+a}）=\frac{1+f（x）}{1-f（x）}$，x∈R，（a是非零常数），则函数y=f（x）的周期是4|a|．
19．求经过点$C（{6，\frac{π}{6}}）$，且平行于极轴的直线的极坐标方程．
9．已知P，A，B是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$上不同的三点，且A，B关于原点对称，若直线PA，PB的斜率乘积${k_{PA}}•{k_{PB}}=\frac{3}{4}$，则该双曲线的离心率是（　　）
A．2B．$\frac{{\sqrt{3}}}{2}$C．$\frac{{\sqrt{7}}}{2}$D．$2\sqrt{2}$
16．设数列{an}是等比数列，且an＞0，Sn为其前n项和．已知a2a4=16，$\frac{{{a_4}+{a_5}+{a_8}}}{{{a_1}+{a_2}+{a_5}}}=8$，则S5等于（　　）
A．40B．20C．31D．43
13．在所有的两位数中，十位数字大于个位数字的两位数共有（　　）
A．50B．45C．36D．35
14．设向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（m，$\sqrt{3}$），且$\overrightarrow{a}$•$\overrightarrow{b}$=2，则实数m=-1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网