题目内容
9.已知P,A,B是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上不同的三点,且A,B关于原点对称,若直线PA,PB的斜率乘积${k_{PA}}•{k_{PB}}=\frac{3}{4}$,则该双曲线的离心率是( )| A. | 2 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $2\sqrt{2}$ |
分析 设出点A,B的坐标,求出斜率,将点的坐标代入方程,两式相减,再结合kPA•kPB=$\frac{3}{4}$,即可求得结论
解答 解:由题意,设A(x1,y1),P(x2,y2),则B(-x1,-y1)
∴kPA•kPB=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}•\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}}=\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$
∵$\frac{{{x}_{1}}^{2}}{{a}^{2}}-\frac{{{y}_{1}}^{2}}{{b}^{2}}=1$,$\frac{{{x}_{2}}^{2}}{{a}^{2}}-\frac{{{y}_{2}}^{2}}{{b}^{2}}=1$,∴两式相减可得$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}=\frac{{b}^{2}}{{a}^{2}}$
∵kPA•kPB=$\frac{3}{4}$,∴$\frac{{b}^{2}}{{a}^{2}}=\frac{3}{4}$,∴,∴e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}=\frac{\sqrt{7}}{2}$.
故选:C.
点评 本题考查双曲线的方程,考查双曲线的几何性质,离心率的求解,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知x与y之间的一组数据:
已求得关于y与x的线性回归方程y=1.2x+0.4,则a的值为2.
| x | 0 | 2 | 4 | 6 |
| y | a | 3 | 5 | 3a |
4.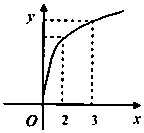 函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
 函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f′(3)<f(3)-f(2)<f′(2) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f(3)-f(2)<f′(2)<f′(3) |
14.平行于直线x+2y+1=0,且与圆x2+y2=5相切的直线的方程是( )
| A. | $x+2y+\sqrt{5}=0$或$x+2y-\sqrt{5}=0$ | B. | $x-2y+\sqrt{5}=0$或$x-2y-\sqrt{5}=0$ | ||
| C. | x+2y+5=0或x+2y-5=0 | D. | x-2y+5=0或x-2y-5=0 |
1.复数z在眏射f下的象为(2+i)z,则1-2i的原象为( )
| A. | -i | B. | i | C. | 4-3i | D. | 4+3i |
19.曲线y=2x-ex在x=0处的切线的倾斜角为( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
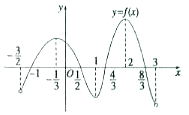 函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).