题目内容
15.设函数f(x)是定义在(0,+∞)上的可导函数,其导函数为f′(x),f(x)>0恒成立,且有2f(x)>xf′(x)+x,则当x>0时,下列不等关系一定正确的是( )| A. | 4xf(x2)≤x4f(2x) | B. | e2xf($\frac{1}{x}$)≥$\frac{1}{{x}^{2}}$f(ex) | ||
| C. | xf($\sqrt{x}$)≤f(x) | D. | 4xf(x+1)≤(x2+2x+1)f(2$\sqrt{x}$) |
分析 x>0时,可得2xf(x)-x2f′(x)>x2>0,令g(x)=$\frac{{x}^{2}}{f(x)}$,则f′(x)=$\frac{2xf(x)-{x}^{2}f′(x)}{{f}^{2}(x)}$>0.即函数g(x)在(0,+∞)单调递增,可得g(x+1)≥g(2$\sqrt{x}$),即可得到结论.
解答 解:当x>0时,有2f(x)>xf′(x)+x恒成立,⇒有2xf(x)-x2f′(x)>x2>0,
令g(x)=$\frac{{x}^{2}}{f(x)}$,则f′(x)=$\frac{2xf(x)-{x}^{2}f′(x)}{{f}^{2}(x)}$>0.
∴函数g(x)在(0,+∞)单调递增,
∵x>0,∴$x+1≥2\sqrt{x}$,即g(x+1)≥g(2$\sqrt{x}$)
⇒$\frac{(x+1)^{2}}{f(x+1)}≥\frac{(2\sqrt{x})^{2}}{f(2\sqrt{x})}$,∵f(x)>0恒成立.∴f(x+1)>0,f(2$\sqrt{x}$)>0,
∴(x+1)2f(2$\sqrt{x}$)≥4xf(x+1).
故选:D.
点评 本题考查了构造新函数,解函数不等式,属于中档题.

练习册系列答案
相关题目
6.“石头、剪刀、布”,又称“猜丁壳”,是一种流传多年的猜拳游戏,起源于中国,然后传到日本、朝鲜等地,随着亚欧贸易的不断发展,它传到了欧洲,到了近代逐渐风靡世界.其游戏规则是:出拳之前双方齐喊口令,然后在话音刚落时同时出拳,握紧的拳头代表“石头”,食指和中指伸出代表“剪刀”,五指伸开代表“布”.“石头”胜“剪刀”、“剪刀”胜“布”、而“布”又胜过“石头”.若所出的拳相同,则为和局.小千和大年两位同学进行“五局三胜制”的“石头、剪刀、布”游戏比赛,则小千和大年比赛至第四局小千胜出的概率是( )
| A. | $\frac{1}{27}$ | B. | $\frac{2}{27}$ | C. | $\frac{2}{81}$ | D. | $\frac{8}{81}$ |
3.已知函数f(x)=-2tan(2x+φ)(|φ|<π),若$f(\frac{π}{16})=-2$,则f(x)的一个单调递减区间是( )
| A. | $(\frac{3π}{16},\frac{11π}{16})$ | B. | $(\frac{π}{16},\frac{9π}{16})$ | C. | $(-\frac{3π}{16},\frac{5π}{16})$ | D. | $(\frac{π}{16},\frac{5π}{16})$ |
4.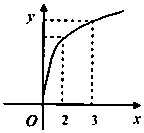 函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
 函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f′(3)<f(3)-f(2)<f′(2) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f(3)-f(2)<f′(2)<f′(3) |