题目内容
13．在所有的两位数中，十位数字大于个位数字的两位数共有（ ）| A． | 50 | B． | 45 | C． | 36 | D． | 35 |
分析 根据题意，按个位数字的不同分9种情况讨论，分别求出每一种情况的符合条件的两位数数目，由分类计数原理计算可得答案．
解答 解：根据题意，按个位数字的不同分9种情况讨论：
①、当个位数字为0时，其十位数字可以为1、2、3、4、5、6、7、8、9，共9种情况；
②、当个位数字为1时，其十位数字可以为2、3、4、5、6、7、8、9，共8种情况；
③、当个位数字为2时，其十位数字可以为3、4、5、6、7、8、9，共7种情况；
④、当个位数字为3时，其十位数字可以为4、5、6、7、8、9，共6种情况；
⑤、当个位数字为4时，其十位数字可以为5、6、7、8、9，共5种情况；
⑥、当个位数字为5时，其十位数字可以为6、7、8、9，共4种情况；
⑦、当个位数字为6时，其十位数字可以为7、8、9，共3种情况；
⑧、当个位数字为7时，其十位数字可以为8、9，共2种情况；
⑨、当个位数字为8时，其十位数字可以为9，共1种情况；
则十位数字大于个位数字的两位数共有9+8+7+6+5+4+3+2+1=45个；
故答案为：45．
点评 本题考查分类计数原理的应用，注意“十位数字大于个位数字”与“十位数字小于个位数字”的个数不等，不能用倍分法分析．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
相关题目
3．已知函数f（x）=-2tan（2x+φ）（|φ|＜π），若$f（\frac{π}{16}）=-2$，则f（x）的一个单调递减区间是（ ）
| A． | $（\frac{3π}{16}，\frac{11π}{16}）$ | B． | $（\frac{π}{16}，\frac{9π}{16}）$ | C． | $（-\frac{3π}{16}，\frac{5π}{16}）$ | D． | $（\frac{π}{16}，\frac{5π}{16}）$ |
4．
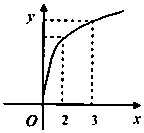函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）
函数f（x）的图象如图所示，f′（x）是f（x）的导函数，则下列数值排序正确的是（ ）| A． | 0＜f′（2）＜f′（3）＜f（3）-f（2） | B． | 0＜f′（3）＜f（3）-f（2）＜f′（2） | C． | 0＜f′（3）＜f′（2）＜f（3）-f（2） | D． | 0＜f（3）-f（2）＜f′（2）＜f′（3） |
1．复数z在眏射f下的象为（2+i）z，则1-2i的原象为（ ）
| A． | -i | B． | i | C． | 4-3i | D． | 4+3i |
8．下表数据为某地区某基地某种农产品的年产量x（单位：吨）及对应销售价格y（单位：万元/吨）．
（1）若y与x有较强的线性相关关系，请用最小二乘法求出y关与x的线性回归方程$\widehaty=\widehatbx+\widehata$；
（2）若每吨该农产品的成本为1万元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润z最大？最大利润是多少？
参考公式：$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{（{{x_i}{y_i}}）}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．
| x | 1 | 2 | 3 |
| y | 5 | 4 | 3 |
（2）若每吨该农产品的成本为1万元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润z最大？最大利润是多少？
参考公式：$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{（{{x_i}{y_i}}）}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．