题目内容
7.已知抛物线y2=6x上的一点到焦点的距离是到y轴距离的2倍,则该点的横坐标为$\frac{3}{2}$.分析 利用抛物线的定义义P到焦点的距离d1=x+$\frac{p}{2}$,P到y轴的距离d2=x,由x+$\frac{3}{2}$=2x,即可求得x值,求得P点的横坐标.
解答 解:抛物线y2=6x焦点F($\frac{3}{2}$,0),设点P(x,y),x>0.
由抛物线的定义P到焦点的距离d1=x+$\frac{p}{2}$=x+$\frac{3}{2}$,
P到y轴的距离d2=x,
由x+$\frac{3}{2}$=2x,解得x=$\frac{3}{2}$,
∴该点的横坐标$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查抛物线的定义,考查计算能力,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
15.已知x∈R,符号[x]表示不超过x的最大整数,f(x)=$\left\{\begin{array}{l}{[x],x≤0}\\{\frac{1}{x},x>0}\end{array}\right.$,则使方程$\frac{f(x)}{x}$=m恰有三个实根的实数m的取值范围是( )
| A. | ($\frac{1}{2}$,$\frac{2}{3}$) | B. | (1,$\frac{3}{2}$) | C. | ($\frac{4}{3}$,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,2) |
19.集合A={x|y=lg(x-2)},B={y|y=2x,x≥0},则(∁RA)∩B=( )
| A. | (0,2) | B. | [0,2] | C. | [1,2] | D. | (1,2) |
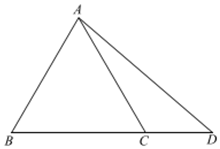 在△ABC中,角A、B、C对边分别为a、b、c,a2+b2+c2=ab+bc+ca.
在△ABC中,角A、B、C对边分别为a、b、c,a2+b2+c2=ab+bc+ca.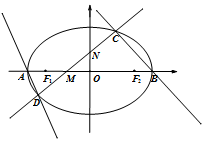 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.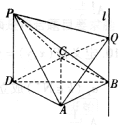 四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点.
四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点.