题目内容
17. 在△ABC中,角A、B、C对边分别为a、b、c,a2+b2+c2=ab+bc+ca.
在△ABC中,角A、B、C对边分别为a、b、c,a2+b2+c2=ab+bc+ca.(1)证明△ABC是正三角形;
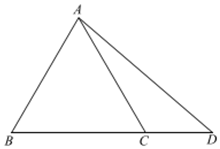
(2)如图,点D在边BC的延长线上,且BC=2CD,AD=$\sqrt{7}$,求sin∠BAD的值.
分析 (1)由已知利用配方法可得(a-b)2+(b-c)2+(c-a)2=0,从而可求a=b=c,即△ABC是正三角形.
(2)由已知可求AC=2CD,∠ACD=120°,由余弦定理可解得CD=1,又BD=3CD=3,由正弦定理可得sin∠BAD
解答 解:(1)证明:∵a2+b2+c2=ab+ac+bc,
∴2a2+2b2+2c2=2ab+2ac+2bc,
(a-b)2+(b-c)2+(a-c)2=0,
∴a=b=c
∴△ABC为等边三角形
(2)∵△ABC是等边三角形,BC=2CD,
∴AC=2CD,∠ACD=120°,
∴在△ACD中,
由余弦定理可得:AD2=AC2+CD2-2AC•CDcos∠ACD,
可得:7=4CD2+CD2-4CD•CDcos120°,解得CD=1,
在△ABC中,BD=3CD=3,由正弦定理可得sin∠BAD=$\frac{BD•sinB}{AD}$=$\frac{3•\frac{\sqrt{3}}{2}}{\sqrt{7}}$=$\frac{3\sqrt{21}}{14}$.
点评 本题主要考查了余弦定理,正弦定理在解三角形中的应用,考查了数形结合思想和配方法的应用,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
7.若函数$f(x)=sin2ωx+2\sqrt{3}{cos^2}ωx-\sqrt{3}(ω>0)$在$[\frac{π}{2},π]$上单调递减,则ω的取值范围是( )
| A. | $[\frac{1}{6},\frac{1}{4}]$ | B. | $[\frac{1}{6},\frac{7}{12}]$ | C. | $[\frac{1}{4},\frac{1}{2}]$ | D. | $[0,\frac{1}{2}]$ |
8.已知a=21.3,b=40.7,c=ln6,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
2.不等式组$\left\{\begin{array}{l}{x≥2}\\{x+y≥6}\\{x-2y≤0}\end{array}\right.$,所表示的平面区域为T,若直线mx-y+m+1=0与T有公共点,实数m的取值范围是( )
| A. | ($\frac{1}{5}$,+∞) | B. | [$\frac{1}{5}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
9.若方程|lnx|=a有两个不等的实根x1和x2,则x1+x2的取值范围是( )
| A. | (1,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (2,+∞) | D. | (0,1) |
6.如图茎叶图表示一次朗诵比赛中甲乙两位选手的得分,则下列说法错误的是( )
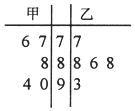

| A. | 甲乙得分的中位数相同 | B. | 乙的成绩较甲更稳定 | ||
| C. | 甲的平均分比乙高 | D. | 乙的平均分低于其中位数 |