题目内容
12.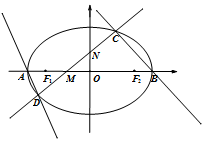 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.(Ⅰ)求椭圆E的离心率;
(Ⅱ)若m>0,设直线AD、BC的斜率分别为k1、k2,求$\frac{k_1}{k_2}$的取值范围.
分析 (Ⅰ)由$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,求出a,c,然后求解椭圆的离心率.
(Ⅱ)设D(x1,y1),C(x2,y2)通过$\left\{{\begin{array}{l}{y=kx+m}\\{{x^2}+4{y^2}=4}\end{array}}\right.$,结合△>0推出m2<4k2+1,利用韦达定理|CM|=|DN|.求出直线的斜率,然后表示出$\frac{k_1}{k_2}$,然后求解它的范围即可.
解答 解:(Ⅰ)由$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,可知$a=2,c=\sqrt{3}$即椭圆方程为$\frac{x^2}{4}+{y^2}=1$…..….(2分)
离心率为$e=\frac{{\sqrt{3}}}{2}$….….(4分)
(Ⅱ)设D(x1,y1),C(x2,y2)易知$A({-2,0}),B({2,0}),N({0,m}),M({-\frac{m}{k},0})$….(5分)
由$\left\{{\begin{array}{l}{y=kx+m}\\{{x^2}+4{y^2}=4}\end{array}}\right.$消去y整理得:(1+4k2)x2+8kmx+4m2-4=0,
由△>0⇒4k2-m2+1>0即m2<4k2+1,${x_1}+{x_2}=\frac{-8km}{{1+4{k^2}}},{x_1}{x_2}=\frac{{4{m^2}-4}}{{1+4{k^2}}}$…(6分)
且|CM|=|DN|即$\overrightarrow{CM}=\overrightarrow{ND}$可知${x_1}+{x_2}=-\frac{m}{k}$,即$\frac{-8km}{{1+4{k^2}}}=-\frac{m}{k}$,解得$k=\frac{1}{2}$….(8分)
${({\frac{k_1}{k_2}})^2}=\frac{{y_1^2{{({{x_2}-2})}^2}}}{{y_2^2{{({{x_1}+2})}^2}}}=\frac{{\frac{4-x_1^2}{4}{{({{x_2}-2})}^2}}}{{\frac{4-x_2^2}{4}{{({{x_1}+2})}^2}}}=\frac{{({2-{x_1}})({2-{x_2}})}}{{({2+{x_1}})({2+{x_2}})}}=\frac{{4-2({{x_1}+{x_2}})+{x_1}{x_2}}}{{4+2({{x_1}+{x_2}})+{x_1}{x_2}}}={({\frac{m+1}{m-1}})^2}$,
由题知,点M、F1的横坐标${x_M}≥{x_{F_1}}$,有$-2m≥-\sqrt{3}$,
易知$m∈({0,\frac{{\sqrt{3}}}{2}}]$满足m2<2,
即$\frac{k_1}{k_2}=-\frac{m+1}{m-1}=-1+\frac{2}{1-m}$,则$\frac{k_1}{k_2}∈({1,7+4\sqrt{3}}]$…..(12分)
点评 本题考查椭圆的简单性质的应用,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案| A. | ($\frac{1}{5}$,+∞) | B. | [$\frac{1}{5}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
| A. | $x-\sqrt{2}y=0$ | B. | $\sqrt{2}x-y=0$ | C. | $\sqrt{2}x±y=0$ | D. | $x±\sqrt{2}y=0$ |
| A. | $\frac{7}{16}$ | B. | $-\frac{2}{5}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |