题目内容

已知F1、F2是双曲线C：
x2
4
-
y2
12
=1的两个焦点，点P是双曲线C上一点，若|PF1|=5，则|PF2|=
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：确定P在双曲线的左支上，由双曲线的定义可得结论．
解答： 解：双曲线C：
x2
4
-
y2
12
=1中a=2，c=
4+12
=4，
∵|PF1|=5＜c+a=6，∴P在双曲线的左支上，
∴由双曲线的定义可得|PF2|-|PF1|=4，
∴|PF2|=9
故答案为：9．
点评：本题考查双曲线的标准方程，考查双曲线的定义，属于基础题．
练习册系列答案
相关题目
如图，在空间四边形ABCD中，AB=BC，CD=DA，E、F、G分别是CD、DA、AC的中点，则（　　）
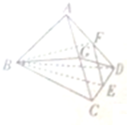
A、平面BEF⊥平面BGD
B、平面ABC⊥平面ACD
C、CD⊥平面BEF
D、AB⊥平面BGD
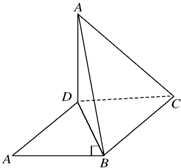在正四棱锥P-ABCD中，若侧面与底面所成二面角的大小为60°，则异面直线PA与BC所成角的正切值等于
 
．
如图，平行四边形ABCD中，AB⊥BD，沿BD将△ABD折起到A′BD，使面A′BD⊥面BCD，连接A′C，则在四面体A′BCD的四个面中，互相垂直的平面有（　　）
①面ABD⊥面BCD；
②面A′CD⊥面ABD；
③面A′BC⊥面BCD；
④面ACD⊥面ABC．
A、1个B、2个C、3个D、4个
从集合{0，1，2，3，4}中随机取出两个不同的数字分别作为点P的横坐标和纵坐标，已知圆C：x2+y2=12．
（1）求点P在圆C内的概率；
（2）若过在圆C内的点P的直线l与圆C分别交于点M，N，当原点到直线l的距离最大时，在圆C内随机撒一粒豆子，求豆子落在△MON（O为原点）内的概率．
判断下列说法正确的是
 
．
①在直线y=xtanα+3中，斜率k=tanα，α为倾斜角
②过点（x1，y1），（x2，y2）所有直线方程为（x2-x1）（y-y1）=（y2-y1）（x-x1）
③a，b为异面直线，与a，b都相交的两条直线l1，l2不可能相交．
④y=
x2-8x+20
+
x2+1
的最小值为5．
⑤P是△ABC所在平面外一点，若点P到三角形的三个顶点的距离相等，则P点的射影为△ABC的外心．
△ABC内接于以O为圆心半径为1的圆，且3
OA
+4
OB
+5
OC
=
0
，则S△AOB=
 
．
长沙市对地铁1、2号线计价“起步价2元可乘6公里采用“递远递减”的计价原则”进行调查，随机抽查了50人，他们月收入的频数分布及对“计价方案”赞成人数如下表．
月收入（单位：百元）[15，25）[25，35）[35，45）[45，55）[55，65）[65，75）
频数510151055
赞成人数4815521
（1）由以上统计数据填写下面2乘2列联表并问是否有99%的把握认为月收入以5500为分界点对“计价方案”的态度有差异：
 月收入不低于55百元的人数月收入低于55百元的人数合计
赞成a=c= 
不赞成b=d= 
合计   
（2）若对月收入在[15，25），[25，35）的被调查人中各随机选取两人进行追踪调查，记选中的四个人中不赞成“计价方案”的人数为ξ，求随机变量ξ的分布列及数学期望．
参考数据：
P（K2≥k）0.0500.0100.001
k3.8416.63510.828
K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
．
已知点D为等腰直角三角形ABC斜边AB的中点，则下列等式中不恒成立的是（　　）
A、
CD
=
CA
|
CA
|
+
CB
|
CB
|
B、
AC
2=
AC
•
AB
C、
BC
2=
BC
•
BA
D、(
CA
+
CB
)•(
CA
-
CB
)=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网