题目内容
已知圆内接四边形ABCD中,AB=3,BC=4,CD=5,AD=6,则cosA= .
考点:余弦定理
专题:计算题,解三角形
分析:连接BD,利用余弦定理求出cosA,cosC的关系,结合圆内接四边形的对角和为180°,运用诱导公式,即可求出cosA的值.
解答:
 解:连接BD,
解:连接BD,
由余弦定理得,BD2=9+36-2×3×6cosA=45-36cosA,
又BD2=16+25-2×4×5cosC=41-40cosC,
∵A+C=180°,∴cosC=-cosA,
∴45-36cosA=41+40cosA,解得cosA=
.
故答案为:
.
 解:连接BD,
解:连接BD,由余弦定理得,BD2=9+36-2×3×6cosA=45-36cosA,
又BD2=16+25-2×4×5cosC=41-40cosC,
∵A+C=180°,∴cosC=-cosA,
∴45-36cosA=41+40cosA,解得cosA=
| 1 |
| 19 |
故答案为:
| 1 |
| 19 |
点评:本题主要考查了余弦定理,以及圆内接四边形的性质:对角互补,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
已知数列{an}为等差数列,a1+a3+a5=-102,a2+a4+a6=-99,以Sn表示{an}的前n项和,则使得Sn达到最小值的n是( )
| A、37和38 | B、38 |
| C、36 | D、36和37 |
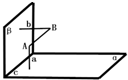 如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.
如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.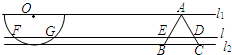 如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧
如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧