题目内容
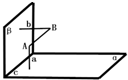如图，已知直线a⊥平面α，b⊥β，且AB⊥a，AB⊥b，平面α∩β=直线c，求证：直线AB∥c．考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由直线a⊥平面α，且AB⊥a，得AB∥平面α．同理AB∥平面β．由此能证明AB∥c．
解答：
解：∵直线a⊥平面α，且AB⊥a，
∴AB∥平面α．
同理直线b⊥平面β，且AB⊥b，
则AB∥平面β．
∵平面α∩β=c，
∴AB∥c．
∴AB∥平面α．
同理直线b⊥平面β，且AB⊥b，
则AB∥平面β．
∵平面α∩β=c，
∴AB∥c．
点评：本题考查直线与平面平行的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
设集合M={4，-3}，N={0，-3}，则M∪N等于（ ）
| A、{-3} |
| B、{0，-3，4} |
| C、{-3，4} |
| D、{0，4} |
下列各对曲线中，即有相同的离心率又有相同渐近线的是（ ）
A、
| ||||||
B、
| ||||||
C、y2-
| ||||||
D、
|