题目内容
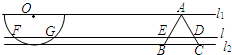 如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧
如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧 |
| FG |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:根据条件求出圆心角∠FOG=x,利用三角关系求出AP=MR=1-cos
,建立函数关系,即可得到结论.
| x |
| 2 |
解答:
解:∵圆的半径为1.∴等边三角形的高为2,即三角形的边长为
,如图所示:
∵ 弧
弧
的弧长为x(0<x<2π),圆的半径为1,
∴圆心角∠FOG=x,即∠FOR=
,
∴OR=OGcos
=cos
,∴MR=1-cos
.
又AP=MR=1-cos
,∠PAE=30°,∴cos30°=
,
∴AD=
=
(1-cos
).
∴y=EB+CD+BC=2(AC-AD)+BC=3AC-2AD=3×
-2AD
=4
-
(1-cos
)=
+
cos
,
故答案为:y=
+
cos
(0<x<π).
4
| ||
| 3 |
∵
 弧
弧 |
| FMG |
∴圆心角∠FOG=x,即∠FOR=
| x |
| 2 |
∴OR=OGcos
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
又AP=MR=1-cos
| x |
| 2 |
| AP |
| AD |
∴AD=
| AP |
| cos30° |
| 2 | ||
|
| x |
| 2 |
∴y=EB+CD+BC=2(AC-AD)+BC=3AC-2AD=3×
4
| ||
| 3 |
=4
| 3 |
| 4 | ||
|
| x |
| 2 |
8
| ||
| 3 |
4
| ||
| 3 |
| x |
| 2 |
故答案为:y=
8
| ||
| 3 |
4
| ||
| 3 |
| x |
| 2 |
点评:本题主要考查函数图象的识别和判断,根据条件建立函数关系是解决本题的关键,综合性较强,难度较大.求出RM=AP是解决本题的关键,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目