题目内容
 如图,在Rt△AOB中,∠OAB=
如图,在Rt△AOB中,∠OAB=| π |
| 6 |
(Ⅰ)求证:平面COD⊥平面AOB;
(Ⅱ)当D为AB的中点时,求异面直线AO与CD所成角的大小;
(Ⅲ)求CD与平面AOB所成角的最大值.
考点:直线与平面所成的角,异面直线及其所成的角,平面与平面垂直的判定
专题:空间角
分析:(Ⅰ)欲证平面COD⊥平面AOB,先证直线与平面垂直,由题意可得:CO⊥AO,BO⊥AO,CO⊥BO,所以CO⊥平面AOB.
(Ⅱ)求异面直线所成的角,需要将两条异面直线平移交于一点,由D为AB的中点,故平移时很容易应联想到中位线,作DE⊥OB,垂足为E,连接CE,则DE∥AO,所以∠CDE是异面直线AO与CD所成的角,利用解三角形的有关知识夹角问题即可.
(Ⅲ)本题的设问是递进式的,第(Ⅰ)问是为第(Ⅲ)问作铺垫的.求直线与平面所成的角,首先要作出这个平面的垂线,由第(1)问可知:CO⊥平面AOB,所以∠CDO是CD与平面AOB所成的角,tan∠CDO=
=
,当OD最小时,∠CDO最大.
(Ⅱ)求异面直线所成的角,需要将两条异面直线平移交于一点,由D为AB的中点,故平移时很容易应联想到中位线,作DE⊥OB,垂足为E,连接CE,则DE∥AO,所以∠CDE是异面直线AO与CD所成的角,利用解三角形的有关知识夹角问题即可.
(Ⅲ)本题的设问是递进式的,第(Ⅰ)问是为第(Ⅲ)问作铺垫的.求直线与平面所成的角,首先要作出这个平面的垂线,由第(1)问可知:CO⊥平面AOB,所以∠CDO是CD与平面AOB所成的角,tan∠CDO=
| OC |
| OD |
| 2 |
| OD |
解答:
解:(Ⅰ)由题意,CO⊥AO,BO⊥AO,
∴∠BOC是二面角B-AO-C是直二面角,
又∵二面角B-AO-C是直二面角,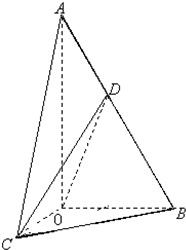
∴CO⊥BO,
又∵AO∩BO=O,
∴CO⊥平面AOB,
∵CO?平面COD,∴平面COD⊥平面AOB
(Ⅱ)作DE⊥OB,垂足为E,连接CE,所以DE∥AO,
∴∠CDE是异面直线AO与CD所成的角.
在 Rt△COE中,CO=BO=2,OE=
BO=1,
∴CE=
=
.
又 DE=
AO=
.
∴CD=
=2
,
∴在Rt△CDE中,cos∠CDE=
=
=
.
∴异面直线AO与CD所成角的大小为arccos
.
(Ⅲ)由(Ⅰ)知,CO⊥平面AOB,
∴∠CDO是CD与平面AOB所成的角,并且tan∠CDO=
=
,
当OD最小时,∠CDO最大,这时,OD⊥AB,垂足为D,
∴OD=
=
,
∴tan∠CDO=
=
,
∴CD与平面AOB所成角的最大值为arctan
.
∴∠BOC是二面角B-AO-C是直二面角,
又∵二面角B-AO-C是直二面角,

∴CO⊥BO,
又∵AO∩BO=O,
∴CO⊥平面AOB,
∵CO?平面COD,∴平面COD⊥平面AOB
(Ⅱ)作DE⊥OB,垂足为E,连接CE,所以DE∥AO,
∴∠CDE是异面直线AO与CD所成的角.
在 Rt△COE中,CO=BO=2,OE=
| 1 |
| 2 |
∴CE=
| CO2+OE2 |
| 5 |
又 DE=
| 1 |
| 2 |
| 3 |
∴CD=
| CE2+DE2 |
| 2 |
∴在Rt△CDE中,cos∠CDE=
| DE |
| CD |
| ||
2
|
| ||
| 4 |
∴异面直线AO与CD所成角的大小为arccos
| ||
| 4 |
(Ⅲ)由(Ⅰ)知,CO⊥平面AOB,
∴∠CDO是CD与平面AOB所成的角,并且tan∠CDO=
| OC |
| OD |
| 2 |
| OD |
当OD最小时,∠CDO最大,这时,OD⊥AB,垂足为D,
∴OD=
| OA•OB |
| AB |
| 3 |
∴tan∠CDO=
| 2 | ||
|
2
| ||
| 3 |
∴CD与平面AOB所成角的最大值为arctan
2
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查异面直线所成的角的大小的求法,考查直线与平面所成角折大小的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
如图给出一个算法的程序框图,该程序框图的功能是( )
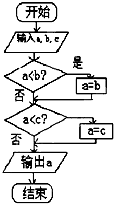

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
已知数列{an},满足an=an-1-3,a2=3,则a9=( )
| A、18 | B、24 |
| C、-18 | D、-21 |
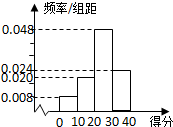 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下: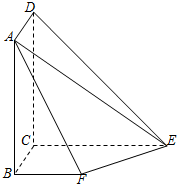 如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.