题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,且经过点(1,
).
(1)求椭圆C的方程;
(2)若点A的坐标为(2,0),直线l经过椭圆C的右焦点F,交椭圆C于P,Q两点.求证:∠PAF=∠QAF.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)若点A的坐标为(2,0),直线l经过椭圆C的右焦点F,交椭圆C于P,Q两点.求证:∠PAF=∠QAF.
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆C:
+
=1(a>b>0)的离心率为
,且经过点(1,
),建立方程组,求出a,b,即可求椭圆C的方程;
(2)分类讨论,斜率不存在时,P,Q关于x轴对称,∠PAF=∠QAF;斜率存在时,设方程为y=k(x-1),直线代入椭圆方程,利用韦达定理,证明kPA+kQA=0即可.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(2)分类讨论,斜率不存在时,P,Q关于x轴对称,∠PAF=∠QAF;斜率存在时,设方程为y=k(x-1),直线代入椭圆方程,利用韦达定理,证明kPA+kQA=0即可.
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)的离心率为
,且经过点(1,
).
∴
,
∴a=
,b=1,
∴椭圆C的方程
+y2=1;
(2)证明:斜率不存在时,P,Q关于x轴对称,∠PAF=∠QAF;
斜率存在时,设方程为y=k(x-1),P(x1,y1),Q(x2,y2),
直线代入椭圆方程可得(1+2k2)x2-4k2x+2k2-2=0,
∴x1+x2=
,x1x2=
,
∴kPA+kQA=
+
=2k+
=2k+
=0,
∴∠PAF=∠QAF,
综上,∠PAF=∠QAF.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
∴
|
∴a=
| 2 |
∴椭圆C的方程
| x2 |
| 2 |
(2)证明:斜率不存在时,P,Q关于x轴对称,∠PAF=∠QAF;
斜率存在时,设方程为y=k(x-1),P(x1,y1),Q(x2,y2),
直线代入椭圆方程可得(1+2k2)x2-4k2x+2k2-2=0,
∴x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∴kPA+kQA=
| y1 |
| x1-2 |
| y2 |
| x2-2 |
| k(x1+x2-4) |
| x1x2-2(x1+x2)+4 |
| k(-4k2-4) |
| 2k2+2 |
∴∠PAF=∠QAF,
综上,∠PAF=∠QAF.
点评:本题考查椭圆的方程与性质,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
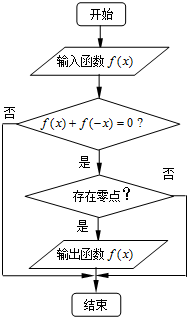 某流程如图所示,现输入四个函数,则可以输出的函数是( )
某流程如图所示,现输入四个函数,则可以输出的函数是( )| A、f(x)=x2 | ||
B、f(x)=
| ||
| C、f(x)=lnx+2x-6 | ||
| D、f(x)=x3 |
已知数列{an},满足an=an-1-3,a2=3,则a9=( )
| A、18 | B、24 |
| C、-18 | D、-21 |
下列各组向量中,可以作为基底的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
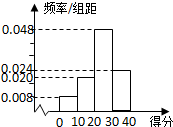 对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下:
对甲、乙两名篮球运动员分别在100场比赛中的得分情况进行统计,做出甲的得分频率分布直方图如图,列出乙的得分统计表如下: