题目内容
如图是一个几何体的三视图,则该几何体的体积是( )


| A、3 | ||
B、
| ||
| C、1 | ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:几何体直四棱柱,根据三视图判断四棱柱的高与底面的形状,根据左视图知底面是等腰梯形,等腰梯形的上、下底边长分别为1、2,由主视图知高为1,把数据代入棱柱的体积公式计算.
解答:
解:由三视图知几何体直四棱柱,且四棱柱的高为2,
底面是等腰梯形,等腰梯形的上、下底边长分别为1、2,高为1,
∴几何体的体积V=
×2=3.
故选:A.
底面是等腰梯形,等腰梯形的上、下底边长分别为1、2,高为1,
∴几何体的体积V=
| 1+2 |
| 2 |
故选:A.
点评:本题考查了由三视图求几何体的体积,判断几何体的形状及数据所对应的几何量是解答此类问题的关键.

练习册系列答案
相关题目
如图给出一个算法的程序框图,该程序框图的功能是( )
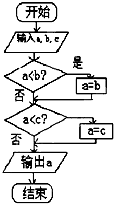

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
已知{an}是由正数组成的等比数列,Sn为其n项和.若a2a4=16,S3=7,则S4=( )
| A、15 | ||
| B、31 | ||
| C、63 | ||
D、
|
若x、y满足不等式
,则z=3x+y的最大值为( )
|
| A、11 | B、-11 |
| C、13 | D、-13 |
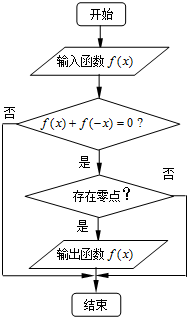 某流程如图所示,现输入四个函数,则可以输出的函数是( )
某流程如图所示,现输入四个函数,则可以输出的函数是( )| A、f(x)=x2 | ||
B、f(x)=
| ||
| C、f(x)=lnx+2x-6 | ||
| D、f(x)=x3 |
已知数列{an},满足an=an-1-3,a2=3,则a9=( )
| A、18 | B、24 |
| C、-18 | D、-21 |
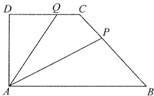 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,