题目内容
若函数f(x)=
存在b∈[0,1],使f(f(b))=b,则实数a的取值范围是 .
| ex+x-a |
考点:函数的值
专题:函数的性质及应用
分析:由f(f(b))=b可得A(b,f(b)),A′(f(b),b)也在函数y=f(x)的图象上为突破即可得到结论.
解答:
解:若存在b∈[0,1],使f(f(b))=b,
则A(b,f(b)),A′(f(b),b)也在函数y=f(x)的图象上,
又f(x)=
在[0,1]上递增,
∴(xA'-xA)(yA'-yA)≥0,
即(f(b)-b)(b-f(b))≥0,
则(f(b)-b)2≤0,
即f(b)=b,即f(x)=x,在[0,1]上有解,
根据 f(x)=
=x,化简整理得ex=x2-x+a,
即a=ex-x2+x,
设F(x)=ex-x2+x,则F′(x)=ex-2x+1≥0,x∈[0,1],
即F(x)在[0,1]上单调递增,
∵F(0)=1,F(1)=e,
∴1≤a≤e
即实数a的取值范围为[1,e]
故答案为:[1,e]
则A(b,f(b)),A′(f(b),b)也在函数y=f(x)的图象上,
又f(x)=
| ex+x-a |
∴(xA'-xA)(yA'-yA)≥0,
即(f(b)-b)(b-f(b))≥0,
则(f(b)-b)2≤0,
即f(b)=b,即f(x)=x,在[0,1]上有解,
根据 f(x)=
| ex+x-a |
即a=ex-x2+x,
设F(x)=ex-x2+x,则F′(x)=ex-2x+1≥0,x∈[0,1],
即F(x)在[0,1]上单调递增,
∵F(0)=1,F(1)=e,
∴1≤a≤e
即实数a的取值范围为[1,e]
故答案为:[1,e]
点评:本题主要考查函数的性质以及导数的有关知识,根据条件转化为函数问题是解决本题的关键.,综合性较强,难度较大.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
已知数列{an},满足an=an-1-3,a2=3,则a9=( )
| A、18 | B、24 |
| C、-18 | D、-21 |
下列各组向量中,可以作为基底的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|

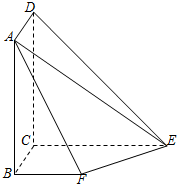 如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.