题目内容
已知函数f(x)=(x2-2x+1)ex(其中e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)定义:若函数h(x)在区间[s,t](s<t)上的取值范围为[s,t],则称区间[s,t]为函数h(x)的“域同区间”.试问函数f(x)在(1,+∞)上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
(1)求函数f(x)的单调区间;
(2)定义:若函数h(x)在区间[s,t](s<t)上的取值范围为[s,t],则称区间[s,t]为函数h(x)的“域同区间”.试问函数f(x)在(1,+∞)上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
考点:利用导数研究函数的单调性,函数单调性的性质,函数零点的判定定理
专题:导数的综合应用
分析:(1)利用函数的正负性,来求原函数的单调区间.
(2)构造新的函数,利用二次求导来判断原函数的单调性,再由特殊值即可判断函数零点的个数.
(2)构造新的函数,利用二次求导来判断原函数的单调性,再由特殊值即可判断函数零点的个数.
解答:
解:(1)因为f(x)=(x2-2x+1)ex,
所以f'(x)=(2x-2)ex+(x2-2x+1)ex=(x2-1)ex=(x+1)(x-1)ex.
当x<-1或x>1时,f'(x)>0,即函数f(x)的单调递增区间为(-∞,-1)和(1,+∞).
当-1<x<1时,f'(x)<0,即函数f(x)的单调递减区间为(-1,1).
所以函数f(x)的单调递增区间为(-∞,-1)和(1,+∞),单调递减区间为(-1,1).
(2)假设函数f(x)在(1,+∞)上存在“域同区间”[s,t](1<s<t),
由(1)知函数f(x)在(1,+∞)上是增函数,
所以
即
也就是方程(x-1)2ex=x有两个大于1的相异实根.
设g(x)=(x-1)2ex-x(x>1),则g'(x)=(x2-1)ex-1.
设h(x)=g'(x)=(x2-1)ex-1,则h'(x)=(x2+2x-1)ex.
因为在(1,+∞)上有h'(x)>0,所以h(x)在(1,+∞)上单调递增.
因为h(1)=-1<0,h(2)=3e2-1>0,
即存在唯一的x0∈(1,2),使得h(x0)=0.
当x∈(1,x0)时,h(x)=g'(x)<0,即函数g(x)在(1,x0)上是减函数;
当x∈(x0,+∞)时,h(x)=g'(x)>0,即函数g(x)在(x0,+∞)上是增函数.
因为g(1)=-1<0,g(x0)<g(1)<0,g(2)=e2-2>0,
所以函数g(x)在区间(1,+∞)上只有一个零点.
这与方程(x-1)2ex=x有两个大于1的相异实根相矛盾,所以假设不成立.
所以函数f(x)在(1,+∞)上不存在“域同区间”.
故答案为:(1)函数f(x)的单调递增区间为(-∞,-1)和(1,+∞),单调递减区间为(-1,1).
(2)函数f(x)在(1,+∞)上不存在“域同区间”.
所以f'(x)=(2x-2)ex+(x2-2x+1)ex=(x2-1)ex=(x+1)(x-1)ex.
当x<-1或x>1时,f'(x)>0,即函数f(x)的单调递增区间为(-∞,-1)和(1,+∞).
当-1<x<1时,f'(x)<0,即函数f(x)的单调递减区间为(-1,1).
所以函数f(x)的单调递增区间为(-∞,-1)和(1,+∞),单调递减区间为(-1,1).
(2)假设函数f(x)在(1,+∞)上存在“域同区间”[s,t](1<s<t),
由(1)知函数f(x)在(1,+∞)上是增函数,
所以
|
|
也就是方程(x-1)2ex=x有两个大于1的相异实根.
设g(x)=(x-1)2ex-x(x>1),则g'(x)=(x2-1)ex-1.
设h(x)=g'(x)=(x2-1)ex-1,则h'(x)=(x2+2x-1)ex.
因为在(1,+∞)上有h'(x)>0,所以h(x)在(1,+∞)上单调递增.
因为h(1)=-1<0,h(2)=3e2-1>0,
即存在唯一的x0∈(1,2),使得h(x0)=0.
当x∈(1,x0)时,h(x)=g'(x)<0,即函数g(x)在(1,x0)上是减函数;
当x∈(x0,+∞)时,h(x)=g'(x)>0,即函数g(x)在(x0,+∞)上是增函数.
因为g(1)=-1<0,g(x0)<g(1)<0,g(2)=e2-2>0,
所以函数g(x)在区间(1,+∞)上只有一个零点.
这与方程(x-1)2ex=x有两个大于1的相异实根相矛盾,所以假设不成立.
所以函数f(x)在(1,+∞)上不存在“域同区间”.
故答案为:(1)函数f(x)的单调递增区间为(-∞,-1)和(1,+∞),单调递减区间为(-1,1).
(2)函数f(x)在(1,+∞)上不存在“域同区间”.
点评:本小题主要考查函数的单调性、函数的导数、函数的零点等知识,考查数形结合、化归与转化、分类与讨论的数学思想方法,以及运算求解能力、抽象概括能力与创新意识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各组向量中,可以作为基底的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
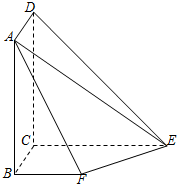 如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,平面ABCD⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.