题目内容
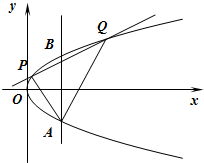 如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=| 1 |
| 2 |
(1)若n=0,∠BAP=∠BAQ,求m的值;
(2)探究:是否存在常数m,当n变化时,恒有∠BAP=∠BAQ?
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由∠BAP=∠BAQ,知kAP+kAQ=0,可得my=2y+m,与y2=m,联立方程组,由此能求出m.
(2)设P(x1,y1),Q(x2,y2),由直线PQ的方程y=
x+n与抛物线y2=x联立,得y2-2y+2n=0.利用韦达定理结合对称性,得到存在常数m,当n变化时,恒有∠BAP=∠BAQ.
(2)设P(x1,y1),Q(x2,y2),由直线PQ的方程y=
| 1 |
| 2 |
解答:
解:(1)由直线PQ的方程y=
x与抛物线y2=x联立,解得P(0,0),Q(4,2).…(2分)
因为∠BAP=∠BAQ,所以kAP+kAQ=0.
设A(m,y),则
+
=0,化简得my=2y+m,…(5分)
又y2=m,联立方程组,解得m=1,或m=4.
因为AB平分∠PAQ,所以m=4不合,故m=1.…(7分)
(2)设P(x1,y1),Q(x2,y2),
由直线PQ的方程y=
x+n与抛物线y2=x联立,得y2-2y+2n=0.
△=4(1-2n),y1+y2=2,y1y2=2n.…(9分)
若存常数m,当n变化时,恒有∠BAP=∠BAQ,则由(1)知只可能m=1.
当m=1时,取A(1,-1),∠BAP=∠BAQ等价于
+
=0,
即(y1+1)(2y2-2n-1)+(y2+1)(2y1-2n-1)=0,
即4y1y2+2(2n+1)=2(n-1)(y1+y2),
即8n=2(2n-1)+2(2n+1),此式恒成立.
∴存在常数m=1,当n变化时,恒有∠BAP=∠BAQ.…(15分).
| 1 |
| 2 |
因为∠BAP=∠BAQ,所以kAP+kAQ=0.
设A(m,y),则
| y |
| m |
| y-2 |
| m-4 |
又y2=m,联立方程组,解得m=1,或m=4.
因为AB平分∠PAQ,所以m=4不合,故m=1.…(7分)
(2)设P(x1,y1),Q(x2,y2),
由直线PQ的方程y=
| 1 |
| 2 |
△=4(1-2n),y1+y2=2,y1y2=2n.…(9分)
若存常数m,当n变化时,恒有∠BAP=∠BAQ,则由(1)知只可能m=1.
当m=1时,取A(1,-1),∠BAP=∠BAQ等价于
| y1+1 |
| x1-1 |
| y2+1 |
| x2-1 |
即(y1+1)(2y2-2n-1)+(y2+1)(2y1-2n-1)=0,
即4y1y2+2(2n+1)=2(n-1)(y1+y2),
即8n=2(2n-1)+2(2n+1),此式恒成立.
∴存在常数m=1,当n变化时,恒有∠BAP=∠BAQ.…(15分).
点评:本题考查直线与椭圆的位置关系的综合应用,综合性质强,难度大,具有一定的探究性,对数学思维的要求较高.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
若x、y满足不等式
,则z=3x+y的最大值为( )
|
| A、11 | B、-11 |
| C、13 | D、-13 |
 已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.
已知四棱锥P-ABCD的底面是平行四边形,AD=2AB,∠ABC=60°,PA⊥面ABCD,且PA=AD.若E为PC中点,F为线段PD上的点,且PF=2FD.