题目内容
计算:
(1)lg
+lg70-lg3;
(2)lg22+lg5lg20-1;
(2)lg52+
lg8+lg5•lg20+(lg2)2.
(1)lg
| 3 |
| 7 |
(2)lg22+lg5lg20-1;
(2)lg52+
| 2 |
| 3 |
考点:对数的运算性质
专题:函数的性质及应用
分析:根据对数的运算法则和对数的换底公式分别进行求解即可.
解答:
解:(1)lg
+lg70-lg3=lg(
×70÷3)=lg10=1;
(2)lg22+lg5lg20-1=lg22+lg5(lg2+1)-1=lg2(lg2+lg5)+lg5-1=lg2+lg5-1=1-1=0;
(2)lg52+
lg8+lg5•lg20+(lg2)2=2lg5+
×3lg2+lg5(lg2+1)+(lg2)2=2lg5+2lg2+lg2(lg5+lg2)+lg5=2(lg5+lg2)+lg2+lg5=2+1=3.
| 3 |
| 7 |
| 3 |
| 7 |
(2)lg22+lg5lg20-1=lg22+lg5(lg2+1)-1=lg2(lg2+lg5)+lg5-1=lg2+lg5-1=1-1=0;
(2)lg52+
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查对数的基本运算,要求熟练掌握对数的四则运算法则和对数的换底公式,比较基础.

练习册系列答案
相关题目
函数f(x)=-|x-5|+2x-1的零点所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
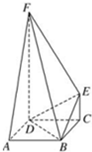 如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.
如图,FD垂直于矩形ABCD所在平面,CE∥DF,∠DEF=90°.