题目内容
已知α=
，则
+
+
+
= ．
| π |
| 24 |
| sinα |
| cos4αcos3α |
| sinα |
| cos3αcos2α |
| sinα |
| cos2αcosα |
| sinα |
| cosα |
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：首先利用提公因式法对关系式进行恒等变换，进一步利用倍角公式及和差化积公式进行恒等变换，最后求的结果．
解答：
解：
+
+
+
=
(
+
)+
(1+
)
=
•
+
•
=
•
+
•
=
+
=
•
=
•
=
=tan4α
由于α=
所以tan4α=tan
=
故答案为：
| sinα |
| cos4αcos3α |
| sinα |
| cos3αcos2α |
| sinα |
| cos2αcosα |
| sinα |
| cosα |
| sinα |
| cos3α |
| 1 |
| cos4α |
| 1 |
| cos2α |
| sinα |
| cosα |
| 1 |
| cos2α |
=
| sinα |
| cos3α |
| cos4α+cos2α |
| cos4α•cos2α |
| sinα |
| cosα |
| 1+cos2α |
| cos2α |
| sinα |
| cos3α |
| 2cos3αcos2α |
| cos4α•cos2α |
| sinα |
| cosα |
| 1+2cos2α-1 |
| cos2α |
=
| sin2α |
| cos4αcos2α |
| sin2α |
| cos2α |
| sin2α |
| cos2α |
| cos4α+1 |
| cos4α |
| sin2α |
| cos2α |
| 2cos22α-1+1 |
| cos4α |
| sin4α |
| cos4α |
由于α=
| π |
| 24 |
所以tan4α=tan
| π |
| 6 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查的知识要点：倍角公式，和差化积公式，同角三角恒等式的应用．
练习册系列答案
相关题目
已知实数a，b，c，d成等比数列，且曲线y=3x-x3的极大值点坐标为（b，c）则ad等于（ ）
| A、2 | B、1 | C、-1 | D、-2 |
命题“函数y=f（x）的导函数为f′（x）=ex+
-
（其中e为自然对数的底数，k为实数），且f（x）在R上不是单调函数”是真命题，则实数k的取值范围是（ ）
| k2 |
| ex |
| 1 |
| k |
A、（-∞，-
| ||||
B、（-
| ||||
C、（0，
| ||||
D、（
|
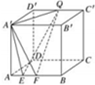如图，正方体ABCD-A′B′C′D′的棱长为4，动点E，F在棱AB上，且EF=2，动点Q在棱D′C′上，则三棱锥A′-EFQ的体积（ ）| A、与点E，F位置有关 |
| B、与点Q位置有关 |
| C、与点E，F，Q位置有关 |
| D、与点E，F，Q位置均无关，是定值 |